题目内容
计算:
(1)(-3x3y2)3•(-4x2y)2÷(-36x4y5)
(2)(-a+2b)(-a-2b)-(2a-3b)2+3a(a-4b)
(1)(-3x3y2)3•(-4x2y)2÷(-36x4y5)
(2)(-a+2b)(-a-2b)-(2a-3b)2+3a(a-4b)
考点:整式的混合运算
专题:
分析:(1)先算乘方,再算乘法,最后算除法;
(2)利用完全平方公式、平方差公式和整式的乘法计算方法计算,再进一步合并即可.
(2)利用完全平方公式、平方差公式和整式的乘法计算方法计算,再进一步合并即可.
解答:解:(1)原式=-27x9y6•16x4y2÷(-36x4y5)
=12x9y3;
(2)原式=a2-4b2-4a2+12ab-9b2+3a2-12ab
=-13b2.
=12x9y3;
(2)原式=a2-4b2-4a2+12ab-9b2+3a2-12ab
=-13b2.
点评:此题考查整式的混合运算,掌握运算顺序,正确判定运算符号,利用计算公式和计算方法是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列语句中,属于命题的是( )
| A、作线段的垂直平分线 |
| B、等角的补角相等吗 |
| C、三角形是轴对称图形 |
| D、用三条线段去拼成一个三角形 |
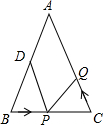 如图,在△ABC中,AB=AC=10,BC=8,点D为AB的中点,如果点P在线段BC上以每秒3个单位长度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动.在某一时刻,△BPD与△CQP全等,此时点Q的运动速度为每秒( )个单位长度.
如图,在△ABC中,AB=AC=10,BC=8,点D为AB的中点,如果点P在线段BC上以每秒3个单位长度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动.在某一时刻,△BPD与△CQP全等,此时点Q的运动速度为每秒( )个单位长度.| A、3 | ||
B、
| ||
| C、3或3.75 | ||
| D、2或3 |
 如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断中,不正确的是( )
如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断中,不正确的是( )| A、a>0 |
| B、b>0 |
| C、c<0 |
| D、b2-4ac>0 |
抛物线y=-
(x+1)2的对称轴是( )
| 1 |
| 2 |
A、直线x=
| ||
| B、直线x=1 | ||
| C、直线x=-1 | ||
| D、直线x=2 |
已知某船在静水中的速度是x千米/小时,水流速度是y千米/小时,该船从甲地到乙地逆水航行a小时可以到达,则船从乙地到甲地所需时间为( )小时.
A、
| ||
B、
| ||
C、
| ||
D、
|
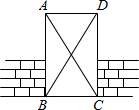 如图所示,工人师傅将门砌到一定高度时,质检员要测一下门的四个角是否都为直角,请你帮质检员想一个检测的办法,并说明理由.
如图所示,工人师傅将门砌到一定高度时,质检员要测一下门的四个角是否都为直角,请你帮质检员想一个检测的办法,并说明理由.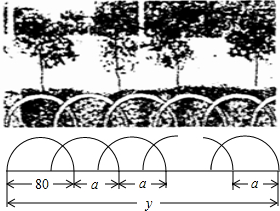 如图,某花园护栏是用直径为80厘米的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度就增加a厘米(a>0).设半圆形条钢的总个数为x(x为正整数),护栏总长度为y厘米.
如图,某花园护栏是用直径为80厘米的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度就增加a厘米(a>0).设半圆形条钢的总个数为x(x为正整数),护栏总长度为y厘米.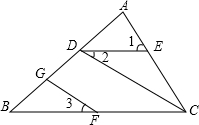 已知:如图,∠1=∠ACB,∠2=∠3,求证:∠BOC+∠DGF=180°.
已知:如图,∠1=∠ACB,∠2=∠3,求证:∠BOC+∠DGF=180°.