题目内容
已知m、n为整数,且m2-n2-8=0(n>0),则mn+1= .
考点:因式分解的应用
专题:
分析:首先因式分解,得到关于m、n的方程组,求出m、n即可解决问题.
解答:解:∵m2-n2-8=0,
∴(m+n)(m-n)=2×4或1×8,
∵m、n为整数,且n>0,
∴①
或②
,
解①得:
,
解②得:
(不合题意,舍去),
∴mn+1=32=9,
故答案为9.
∴(m+n)(m-n)=2×4或1×8,
∵m、n为整数,且n>0,
∴①
|
|
解①得:
|
解②得:
|
∴mn+1=32=9,
故答案为9.
点评:该题主要考查了因式分解及其应用问题;解题的关键是灵活运用因式分解法将所给的等式恒等变形,借助整数的性质列出关于m、n的方程组,求出m、n.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
抛物线y=-
(x+1)2的对称轴是( )
| 1 |
| 2 |
A、直线x=
| ||
| B、直线x=1 | ||
| C、直线x=-1 | ||
| D、直线x=2 |
将抛物线y=(x+1)2-2向上平移2个单位,则平移后抛物线的解析式为( )
| A、y=(x+1)2-2 |
| B、y=(x+1)2 |
| C、y=(x+1)2-4 |
| D、y=(x+1)2-1 |
已知某船在静水中的速度是x千米/小时,水流速度是y千米/小时,该船从甲地到乙地逆水航行a小时可以到达,则船从乙地到甲地所需时间为( )小时.
A、
| ||
B、
| ||
C、
| ||
D、
|
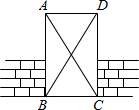 如图所示,工人师傅将门砌到一定高度时,质检员要测一下门的四个角是否都为直角,请你帮质检员想一个检测的办法,并说明理由.
如图所示,工人师傅将门砌到一定高度时,质检员要测一下门的四个角是否都为直角,请你帮质检员想一个检测的办法,并说明理由.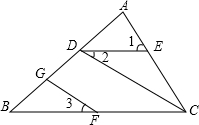 已知:如图,∠1=∠ACB,∠2=∠3,求证:∠BOC+∠DGF=180°.
已知:如图,∠1=∠ACB,∠2=∠3,求证:∠BOC+∠DGF=180°. 如图,直线l1:y=ax,l2:y=kx+b相交于点A,则关于x,y的二元一次方程组
如图,直线l1:y=ax,l2:y=kx+b相交于点A,则关于x,y的二元一次方程组