题目内容
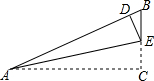 小明在学习“锐角三角函数”中发现,将如图的含30°(∠BAC)角的直角三角形纸片ABC沿过点A的直线折叠,使点C落在AB上的点D处,这样就可以求出75°角的正切值是( )
小明在学习“锐角三角函数”中发现,将如图的含30°(∠BAC)角的直角三角形纸片ABC沿过点A的直线折叠,使点C落在AB上的点D处,这样就可以求出75°角的正切值是( )A、2-
| ||
B、2+
| ||
| C、2.5 | ||
D、
|
考点:解直角三角形
专题:计算题
分析:根据含30度的直角三角形三边的关系设BC=1,则AC=
,AB=2,再根据折叠的性质得∠CAE=
∠CAB=15°,CE=DE,AD=AC=
,则∠AEC=75°,设CE=x,则DE=x,BE=1-x,在Rt△BDE中,根据勾股定理得(1-x)2=x2+(2-
)2,解得x=2
-3,然后在Rt△AEC中,根据正切的定义求解.
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
解答:解:在Rt△ABC中,设BC=1,则AC=
,AB=2,
∵含30°(∠BAC)角的直角三角形纸片ABC沿过点A的直线折叠,使点C落在AB上的点D处,
∴∠CAE=
∠CAB=15°,CE=DE,AD=AC=
,
∴∠AEC=75°,
设CE=x,则DE=x,BE=1-x,
在Rt△BDE中,BD=AB-AD=2-
,
∵BE2=DE2+BD2,
∴(1-x)2=x2+(2-
)2,解得x=2
-3,
在Rt△AEC中,tan∠AEC=tan75°=
=
=2+
.
故选B.
| 3 |
∵含30°(∠BAC)角的直角三角形纸片ABC沿过点A的直线折叠,使点C落在AB上的点D处,
∴∠CAE=
| 1 |
| 2 |
| 3 |
∴∠AEC=75°,
设CE=x,则DE=x,BE=1-x,
在Rt△BDE中,BD=AB-AD=2-
| 3 |
∵BE2=DE2+BD2,
∴(1-x)2=x2+(2-
| 3 |
| 3 |
在Rt△AEC中,tan∠AEC=tan75°=
| AC |
| EC |
| ||
2
|
| 3 |
故选B.
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了折叠的性质.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,E为AD的中点.已知AO=6cm,则AC的长为( )
如图,在平行四边形ABCD中,E为AD的中点.已知AO=6cm,则AC的长为( )| A、12cm | B、10cm |
| C、18cm | D、15cm |
 已知如图直线AB∥CD,∠A=40°且AE=AF,则∠DCF=( )
已知如图直线AB∥CD,∠A=40°且AE=AF,则∠DCF=( )| A、110° | B、120° |
| C、130° | D、140° |
一个空间几何体的主视图和左视图都是边长为4的正方形,俯视图是一个圆,那么这个几何体的表面积是( )
| A、24π | B、64π |
| C、32π | D、48π |
 如图,已知AB∥CD,则图中与∠1互补的角有( )
如图,已知AB∥CD,则图中与∠1互补的角有( )| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在面板上有4个开关,分别控制2盏电灯和2只吊扇,随意按下一只开关,电灯亮的概率是
如图,在面板上有4个开关,分别控制2盏电灯和2只吊扇,随意按下一只开关,电灯亮的概率是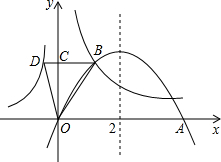 如图,对称轴为x=2的抛物线y=ax2+bx(a≠0)与x轴交于原点O与点A,与反比例函数
如图,对称轴为x=2的抛物线y=ax2+bx(a≠0)与x轴交于原点O与点A,与反比例函数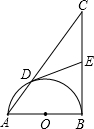 如图,已知直角△ABC中,∠ABC=90°,以AB为直径的⊙O与AC交于点D,点E在线段BC上且DE=BE.
如图,已知直角△ABC中,∠ABC=90°,以AB为直径的⊙O与AC交于点D,点E在线段BC上且DE=BE.