题目内容
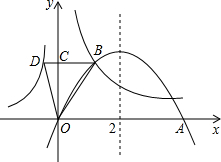 如图,对称轴为x=2的抛物线y=ax2+bx(a≠0)与x轴交于原点O与点A,与反比例函数y=
如图,对称轴为x=2的抛物线y=ax2+bx(a≠0)与x轴交于原点O与点A,与反比例函数y=| b |
| x |
| a |
| x |
①ab>0; ②方程ax2+bx=0的两根为0和4;
③3a+b<0; ④tan∠BOC=4tan∠COD
正确的有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:反比例函数综合题
专题:
分析:①由反比例函数y=
(x>0)在第一象限,反比例函数y=
在第二象限,可得b>0,a<0,即可判定ab<0;
②由对称轴为x=2的抛物线y=ax2+bx(a≠0)与x轴交于原点O与点A,即可求得点A的坐标,继而求得方程ax2+bx=0的两根为0和4;
③由将A(4,0)代入抛物线y=ax2+bx得:16a+4b=0,可得b=-4a,即可判定3a+b=3a-4a=-a>0;
④由③易得tan∠BOC=4tan∠COD.
| b |
| x |
| a |
| x |
②由对称轴为x=2的抛物线y=ax2+bx(a≠0)与x轴交于原点O与点A,即可求得点A的坐标,继而求得方程ax2+bx=0的两根为0和4;
③由将A(4,0)代入抛物线y=ax2+bx得:16a+4b=0,可得b=-4a,即可判定3a+b=3a-4a=-a>0;
④由③易得tan∠BOC=4tan∠COD.
解答:解:①∵反比例函数y=
(x>0)在第一象限,反比例函数y=
在第二象限,
∴b>0,a<0,
∴ab<0,故①错误;
②∵对称轴为x=2的抛物线y=ax2+bx(a≠0)与x轴交于原点O与点A,
∴点A(4,0),
∴方程ax2+bx=0的两根为0和4;故②正确;
③将A(4,0)代入抛物线y=ax2+bx得:16a+4b=0,
∴b=-4a,
∴3a+b=3a-4a=-a>0;故③错误;
④∵点B与D纵坐标相等,
∴设点B(
,y),点D(
,y),
∴tan∠BOC=
=
,tan∠COD=-
,
∵b=-4a,
∴tan∠BOC=4tan∠COD.故④正确.
故选C.
| b |
| x |
| a |
| x |
∴b>0,a<0,
∴ab<0,故①错误;
②∵对称轴为x=2的抛物线y=ax2+bx(a≠0)与x轴交于原点O与点A,
∴点A(4,0),
∴方程ax2+bx=0的两根为0和4;故②正确;
③将A(4,0)代入抛物线y=ax2+bx得:16a+4b=0,
∴b=-4a,
∴3a+b=3a-4a=-a>0;故③错误;
④∵点B与D纵坐标相等,
∴设点B(
| b |
| y |
| a |
| y |
∴tan∠BOC=
| BC |
| OC |
| b |
| y2 |
| a |
| y2 |
∵b=-4a,
∴tan∠BOC=4tan∠COD.故④正确.
故选C.
点评:此题考查了反比例函数的性质、二次函数的性质以及三角函数等知识.此题综合性较强,难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=| k |
| x |
| A、-2 | B、-4 | C、4 | D、-8 |
在同一平面内有直线a1,a2,a3,…,a2012,a2013,a1∥a2,a2⊥a3,a3∥a4,a4⊥a5,…,按此规律,那么a1与a2014的位置关系是( )
| A、平行 | B、垂直 |
| C、相交 | D、无法判断 |
关于未知数x的方程ax2-
x-1=0有两个实数解,则a的取值范围是( )
| 5-a |
A、a≥-
| ||
| B、0<a≤5 | ||
C、-
| ||
| D、0<a≤5,且a≠0 |
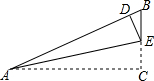 小明在学习“锐角三角函数”中发现,将如图的含30°(∠BAC)角的直角三角形纸片ABC沿过点A的直线折叠,使点C落在AB上的点D处,这样就可以求出75°角的正切值是( )
小明在学习“锐角三角函数”中发现,将如图的含30°(∠BAC)角的直角三角形纸片ABC沿过点A的直线折叠,使点C落在AB上的点D处,这样就可以求出75°角的正切值是( )A、2-
| ||
B、2+
| ||
| C、2.5 | ||
D、
|
 如图是有关x的代数式的方阵,若第10行第2项的值为1034,则此时x的值为( )
如图是有关x的代数式的方阵,若第10行第2项的值为1034,则此时x的值为( )| A、10 | B、1 | C、5 | D、2 |
