题目内容
如图，在平行四边形ABCD中，E为AD的中点．已知AO=6cm，则AC的长为（ ）| A、12cm | B、10cm |
| C、18cm | D、15cm |
考点：平行四边形的性质,相似三角形的判定与性质
专题：
分析：首先证明△AOE∽△COB，利用相似三角形的性质，可求出OC，继而可得AC的长度．
解答：解：∵四边形ABCD是平行四边形，
∴AE∥BC，
∴△AOE∽△COB，
∴
=
，
∵E为AD的中点，AD=BC
∴
=
=
，
∴OC=12cm，
∴AC=AO+OC=18cm．
故选C．
∴AE∥BC，
∴△AOE∽△COB，
∴
| AE |
| BC |
| AO |
| OC |
∵E为AD的中点，AD=BC
∴
| AE |
| BC |
| AO |
| OC |
| 1 |
| 2 |
∴OC=12cm，
∴AC=AO+OC=18cm．
故选C．
点评：本题考查了平行四边形的性质、相似三角形的判定与性质，解答本题的关键是熟练相似三角形的对应边成比例．
练习册系列答案
相关题目
在同一平面内有直线a1，a2，a3，…，a2012，a2013，a1∥a2，a2⊥a3，a3∥a4，a4⊥a5，…，按此规律，那么a1与a2014的位置关系是（ ）
| A、平行 | B、垂直 |
| C、相交 | D、无法判断 |
如图，已知⊙O1的半径为1cm，⊙O2的半径为4cm，将⊙O1，⊙O2放置在直线l上，如果⊙O1在直线l上任意滚动，那么圆心距O1O2的长不可能是（ ）| A、6cm | B、5cm |
| C、3cm | D、2cm |
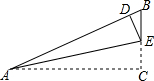小明在学习“锐角三角函数”中发现，将如图的含30°（∠BAC）角的直角三角形纸片ABC沿过点A的直线折叠，使点C落在AB上的点D处，这样就可以求出75°角的正切值是（ ）A、2-
| ||
B、2+
| ||
| C、2.5 | ||
D、
|
下列等式错误的是（ ）
| A、（-2）0=1 |
| B、（-1）-2=-1 |
| C、（-2）4÷（-2）2=4 |
| D、（-2）3•（-2）3=26 |
一个圆锥的三视图如图，则此圆锥的侧面积为（ ）
| A、15πcm2 |
| B、30πcm2 |
| C、45πcm2 |
| D、55πcm2 |
