题目内容
18．方程组$\left\{\begin{array}{l}{|x+1|=4}\\{{x}^{2}=2x+3}\end{array}\right.$的解是（ ）| A． | -1 | B． | 3 | C． | -1或3 | D． | -5或3 |
分析 根据绝对值的意义解第一个方程得到得x=3或x=-5，再利用因式分解法解第二个方程得到x1=-1，x2=3，然后找出两个方程的公共解即可得到方程组的解．
解答 解：解|x+1|=4得x=3或x=-5，
解x2=2x+3得x1=-1，x2=3，
所以方程组得解为x=3．
故选B．
点评 本题考查了解一元二次方程-因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．
练习册系列答案
互动英语系列答案
相关题目
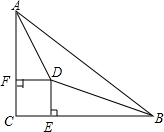如图所示△ABC中，∠C=90°，∠A，∠B的平分线交于D点，DE⊥BC于点E，DF⊥AC于点F．
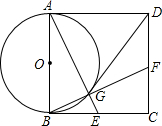如图，在正方形ABCD中，G是以AB为直径的圆上一点，连接AG并延长交BC于点E，连接BG并延长交CD于点F．
如图，在直角梯形ABCD中，∠ABC=90°，AD∥BC，以AB为直径作⊙O恰好与CD相切．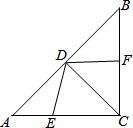
如图，在Rt△ABC中，∠ACB=90°，AC=BC，CD是∠ACB的角平分线，点E、F分别是边AC、BC上的动点．AB=$\sqrt{32}$，设AE=x，BF=y．
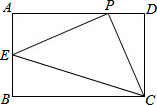已知在矩形ABCD中，AB=2，BC=3，P是AD边上任意一点，（不含端点A、D），连接PC，过点P作PE⊥PC交AB于点E，在点P运动过程中，连接EC，是否存在∠ECP=∠DCP的情况？若存在，求出此时BE的长；若不存在，请说明理由．
8．△ABC的一边长为5，另两边分别是方程x2-6x+m=0的两根，则m的取值范围是（ ）
| A． | m＞$\frac{11}{4}$ | B． | $\frac{11}{4}$＜m≤9 | C． | $\frac{11}{4}$≤m≤9 | D． | m≤$\frac{11}{4}$ |