题目内容
2.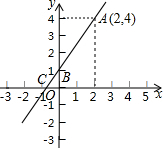 如图,一次函数y=ax+b的图象经过A、B两点,与x轴交于点C.
如图,一次函数y=ax+b的图象经过A、B两点,与x轴交于点C.(1)求直线AC的函数表达式;
(2)设点(a,-2)在这个函数图象上,求a的值.
分析 (1)一次函数y=kx+b的图象经过A、B两点,即A(2,4),B(0,1),代入可求出函数关系式;
(2)把点(a,-2)代入(1)中求得得解析式,即可求得a的值.
解答 解:一次函数y=kx+b的图象经过A、B两点,由图可知A(2,4),B(0,1),
可得出方程组$\left\{\begin{array}{l}{2k+b=4}\\{b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=1}\end{array}\right.$,
则此一次函数的解析式为y=$\frac{3}{2}$x+1;
(2)把点(a,-2)代入y=$\frac{3}{2}$x+1,得,-2=$\frac{3}{2}$a+1,
解得a=-2.
点评 本题主要考查了用待定系数法求一次函数的解析式以及一次函数图象上点的坐标特征,熟练掌握待定系数法是关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
13.关于x的一元二次方程(m-3)x2+2x-1=0有实数根,则m的取值范围是( )
| A. | m≥2 | B. | m>2 | C. | m≥2且m≠3 | D. | m>2且m≠3 |
13.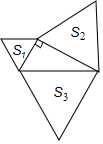 如图,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3.其中S1=4,S2=12,则S3=( )
如图,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3.其中S1=4,S2=12,则S3=( )
 如图,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3.其中S1=4,S2=12,则S3=( )
如图,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3.其中S1=4,S2=12,则S3=( )| A. | 8 | B. | 16 | C. | 160 | D. | 128 |
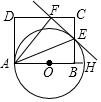 如图,AH是⊙O的直径,矩形ABCD交⊙O于点E,连接AE,将矩形ABCD沿AE折叠,点B落在CD边上的点F处,画直线EF.
如图,AH是⊙O的直径,矩形ABCD交⊙O于点E,连接AE,将矩形ABCD沿AE折叠,点B落在CD边上的点F处,画直线EF. 如图所示,△ABC两个外角的平分线BP、CP相交于点P.
如图所示,△ABC两个外角的平分线BP、CP相交于点P. 如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=8,DE=2,AB=5,则AC长是( )
如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=8,DE=2,AB=5,则AC长是( ) 如图,AB是⊙O的直径,点C是半圆上的一个三等分点,点D是$\widehat{AC}$的中点,点P是直径AB上一点,若⊙O的半径为2,则PC+PD的最小值是2$\sqrt{2}$.
如图,AB是⊙O的直径,点C是半圆上的一个三等分点,点D是$\widehat{AC}$的中点,点P是直径AB上一点,若⊙O的半径为2,则PC+PD的最小值是2$\sqrt{2}$.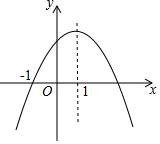 二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,下列结论:①abc<0;②2a+b<0;③b2-4ac=0;④8a+c<0;⑤a:b:c=-1:2:3,其中正确的结论有①④⑤.
二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,下列结论:①abc<0;②2a+b<0;③b2-4ac=0;④8a+c<0;⑤a:b:c=-1:2:3,其中正确的结论有①④⑤.