题目内容
14. 如图,AB是⊙O的直径,点C是半圆上的一个三等分点,点D是$\widehat{AC}$的中点,点P是直径AB上一点,若⊙O的半径为2,则PC+PD的最小值是2$\sqrt{2}$.
如图,AB是⊙O的直径,点C是半圆上的一个三等分点,点D是$\widehat{AC}$的中点,点P是直径AB上一点,若⊙O的半径为2,则PC+PD的最小值是2$\sqrt{2}$.
分析 作D关于AB的对称点E,连接CE交AB于点P′,连接OC,OE,则DP+CP最小,根据解直角三角形求出CE,根据轴对称求出DP′+CP′=CE即可.
解答 解:作D关于AB的对称点E,连接CE交AB于点P′,连接OC,OE,
则根据垂径定理得:E在⊙O上,连接EC交AB于P′,则若P在P′时,DP+CP最小,
∵C是半圆上的一个三等分点,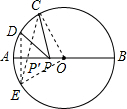
∴∠AOC=$\frac{1}{3}$×180°=60°,
∵D是$\widehat{AC}$的中点,
∴∠AOE=$\frac{1}{2}$∠AOC=30°,
∴∠COE=90°,
∴CE=$\sqrt{2}$OC=2$\sqrt{2}$,
即DP+CP=2$\sqrt{2}$,
故答案为2$\sqrt{2}$.
点评 本题考查了解直角三角形,圆周角定理,垂径定理,轴对称的性质等知识点的应用,主要考查学生的推理和计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.若|a+2|+(b-3)2=0,则ab的值为( )
| A. | 6 | B. | -6 | C. | 1 | D. | -5 |
19.现有相同个数的甲、乙两组数据,经计算得:$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,且S甲2=0.35,S乙2=0.25,比较这两组数据的稳定性,下列说法正确的是( )
| A. | 甲比较稳定 | B. | 乙比较稳定 | C. | 甲、乙一样稳定 | D. | 无法确定 |
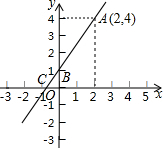 如图,一次函数y=ax+b的图象经过A、B两点,与x轴交于点C.
如图,一次函数y=ax+b的图象经过A、B两点,与x轴交于点C. 如图,在三角形ABC中,∠BAC=130°,DE、FG分别垂直平分边AB和AC,那么∠DAF=80°.
如图,在三角形ABC中,∠BAC=130°,DE、FG分别垂直平分边AB和AC,那么∠DAF=80°.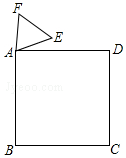 如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小是15°或165°.
如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小是15°或165°.