题目内容
13.关于x的一元二次方程(m-3)x2+2x-1=0有实数根,则m的取值范围是( )| A. | m≥2 | B. | m>2 | C. | m≥2且m≠3 | D. | m>2且m≠3 |
分析 根据二次项系数非零结合根的判别式△≥0,即可得出关于m的一元一次不等式组,解之即可得出结论.
解答 解:∵关于x的一元二次方程(m-3)x2+2x-1=0有实数根,
∴$\left\{\begin{array}{l}{m-3≠0}\\{△={2}^{2}+4(m-3)≥0}\end{array}\right.$,
解得:m≥2且m≠3.
故选C.
点评 本题考查了根的判别式以及一元二次方程的定义,根据二次项系数非零结合根的判别式△≥0,列出关于m的一元一次不等式组是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
3.在一个不透明的袋中装有2个黄球和2个红球,它们除颜色外没有其他区别,从袋中任意摸出一个球,然后放回搅匀,再从袋中任意摸出一个球,那么两次都摸到黄球的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
8.已知n是自然数,且$\frac{20n+17}{13n+4}$能约分,则n最小是( )
| A. | 3 | B. | 2 | C. | 1 | D. | 非上述答案 |
5.若|a+2|+(b-3)2=0,则ab的值为( )
| A. | 6 | B. | -6 | C. | 1 | D. | -5 |
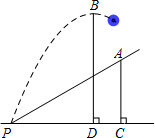 如图,小明在一次高尔夫球训练中,从山坡下P点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度BD为10米时,球移动的水平距离PD为8米,已知山坡PA与水平方向PC的夹角为45°,AC⊥PC于点C,P、A两点相距10$\sqrt{2}$米.请你以P为原点,直线PC为x轴建立适当的平面直角坐标系解决下列问题.
如图,小明在一次高尔夫球训练中,从山坡下P点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度BD为10米时,球移动的水平距离PD为8米,已知山坡PA与水平方向PC的夹角为45°,AC⊥PC于点C,P、A两点相距10$\sqrt{2}$米.请你以P为原点,直线PC为x轴建立适当的平面直角坐标系解决下列问题.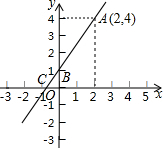 如图,一次函数y=ax+b的图象经过A、B两点,与x轴交于点C.
如图,一次函数y=ax+b的图象经过A、B两点,与x轴交于点C.