题目内容
3.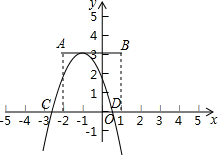 已知点A,B的坐标分别为(-2,3)和(1,3),平移抛物线y=ax2+bx+c(a<0),该抛物线的顶点在线段AB上运动,与x轴交于C、D两点.
已知点A,B的坐标分别为(-2,3)和(1,3),平移抛物线y=ax2+bx+c(a<0),该抛物线的顶点在线段AB上运动,与x轴交于C、D两点.(1)点C横坐标的最大值是1-$\sqrt{-\frac{3}{a}}$;
(2)若四边形ACDB为平行四边形,则a的值是-$\frac{3}{4}$.
分析 (1)当点C横坐标取得最大值时,抛物线顶点坐标是(1,3),根据顶点公式求得b=-2a,b2-4ac=-12a,然后根据交点坐标公式得出C横坐标的最大值.
(2)若四边形ACDB为平行四边形,则CD=AB=3,设此时C(x1,0),D(x2,0),根据二次函数和方程的关系得出x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,根据矩形的性质得出|x1-x2|=3,经过变形即可求得a的值.
解答 解:(1)∵抛物线的顶点在线段AB上运动,
∴当顶点运动到B(1,3)时,点C的横坐标最大,
∴-$\frac{b}{2a}$=1,$\frac{4ac-{b}^{2}}{4a}$=3,
∴b=-2a,b2-4ac=-12a,
∴x=$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{2a-\sqrt{-12a}}{2a}$=$\frac{2a-2\sqrt{-3a}}{2a}$=1-$\sqrt{-\frac{3}{a}}$
即C的横坐标的最大值是1-$\sqrt{-\frac{3}{a}}$;
故答案为1-$\sqrt{-\frac{3}{a}}$;
(2)若四边形ACDB为平行四边形,则CD=AB=3,
设此时C(x1,0),D(x2,0),
∴x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,
∴|x1-x2|=$\sqrt{({{x}_{1}}^{2}+{{x}_{2}}^{2})-4{x}_{1}{x}_{2}}$=$\sqrt{(-\frac{b}{a})^{2}-4×\frac{c}{a}}$=3,
∵顶点的纵坐标为$\frac{4ac-{b}^{2}}{4a}$=3,
∴b2-4ac=-12a,
∴$\sqrt{-\frac{12}{a}}$=3,
∴9a=-12,解得a=-$\frac{3}{4}$.
故答案为-$\frac{3}{4}$.
点评 本题考查了二次函数的图象与几何变换,平行四边形的性质,理解题意并根据二次函数和方程的关系列出关系式是解此题的关键,此题是一个比较典型的题目.

| A. | 8 | B. | 10 | C. | 8或10 | D. | 6或10 |
| A. | (4,0) | B. | (0,0) | C. | (2,2$\sqrt{3}$) | D. | (4,$\sqrt{3}$) |
 如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )
如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )



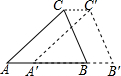 如图,将三角形ABC沿AB方向平移至三角形A1B1C1的位置,连接CC1,AB=5cm,A1B=3cm,∠ABC=35°,CC1=2cm,∠C1CB=35°.
如图,将三角形ABC沿AB方向平移至三角形A1B1C1的位置,连接CC1,AB=5cm,A1B=3cm,∠ABC=35°,CC1=2cm,∠C1CB=35°.