题目内容
16.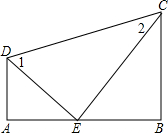 已知:如图,DA⊥AB,DE平分∠ADC,CE平分∠BCD,且∠DEC=90°.试猜想BC与AB有怎样的位置关系,并说明其理由.
已知:如图,DA⊥AB,DE平分∠ADC,CE平分∠BCD,且∠DEC=90°.试猜想BC与AB有怎样的位置关系,并说明其理由.
分析 根据角平分线的定义求出∠ADC=2∠1,∠BCD=2∠2,然后根据∠DEC=90°得出∠1+∠2=90°,即可求出∠ADC+∠BCD=180°,再根据同旁内角互补,两直线平行求出AD∥BC,然后根据两直线平行,同旁内角互补求出∠B=90°,然后即可得解.
解答 解:BC⊥AB.理由如下:
∵DE平分∠ADC,CE平分∠BCD,
∴∠ADC=2∠1,∠BCD=2∠2,
∵∠DEC=90°,
∴∠1+∠2=90°,
∴∠ADC+∠BCD=180°,
∴AD∥BC,
∵DA⊥AB,
∴∠A=90°,
∴∠B=180°-∠A=180°-90°=90°,
∴BC⊥AB.
点评 本题考查了平行线的判定与性质,角平分线的定义,熟记性质与判定方法求出AD∥BC是解题的关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
7.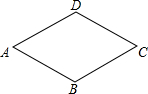 如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )
如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )
 如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )
如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )| A. | 16 | B. | 16$\sqrt{2}$ | C. | 16$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
4.在平面直角坐标系中,第四象限内有一点P,且P点到x轴距离是4,到y轴的距离是5,则点P点坐标为( )
| A. | (4,5) | B. | (4,-5) | C. | (5,4) | D. | (5,-4) |
 如图,若∠1=35°,则∠2=145°,∠3=35°.
如图,若∠1=35°,则∠2=145°,∠3=35°.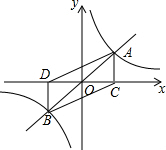 如图,函数y=x与y=$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作x轴垂线,垂足分别为点C、D,则四边形ACBD的面积为8.
如图,函数y=x与y=$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作x轴垂线,垂足分别为点C、D,则四边形ACBD的面积为8.