题目内容
3．
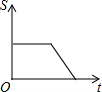如图所示，AB是半圆O的直径，点P从点A出发，沿A→B→O→A的路径运动一周．设OP为s，运动时间为t，则下列图形能大致地刻画s与t之间关系的是（ ）| A． |  | B． |  | C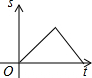． |  | D． |  |
分析 点P在$\widehat{AB}$上运动时，S=OP=$\frac{1}{2}$AB（定值），点P在OB上从点B向O运动的过程中，S随着t的增大而减小，点P在OA上从点O向A运动的过程中，S随着t的增大而增大，即可得到答案．
解答 解：点P在$\widehat{AB}$上运动时，S=OP=$\frac{1}{2}$AB（定值），
点P在OB上从点B向O运动的过程中，S随着t的增大而减小，
点P在OA上从点O向A运动的过程中，S随着t的增大而增大，
故选A．
点评 此题考查了函数随自变量的变化而变化的问题，能够结合图形正确分析距离y与时间x之间的大小变化关系，从而正确选择对应的图象．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
13．下列命题是真命题的是（ ）
| A． | 内错角相等 | |
| B． | 如果a2=b2，那么a3=b3 | |
| C． | 三角形的一个外角大于任何一个内角 | |
| D． | 平行于同一直线的两条直线平行 |
11．已知代数式$\frac{1}{2}$xa-1y3与-3xby2a-b是同类项，那么a，b的值分别是（ ）
| A． | $\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{a=-2}\\{b=-1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$ |
已知：矩形ABCD中，对角线AC与BD交于点O，∠BOC=120°，AC=4cm，求矩形ABCD的周长．
如图，小明把一块含有60°角的直角三角尺的两个顶点放在直尺的对边上，并测得∠1=20°，则∠2的度数是40°．
如图，△ABC中AB=AC=10，BC=16．