题目内容
6.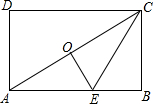 如图,已知矩形ABCD中,点E在AB上,点O是对角线AC的中点,沿CE折叠后,点B恰好与点O重合,若BC=6,则折痕CE的长为( )
如图,已知矩形ABCD中,点E在AB上,点O是对角线AC的中点,沿CE折叠后,点B恰好与点O重合,若BC=6,则折痕CE的长为( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8 | D. | 10 |
分析 由点O是矩形ABCD的中心,E是AB上的点沿CE折叠后,点B恰好与点O重合,可求得∠BAC=30°,继而可得∠BCE=30°,继而求得折痕CE的长.
解答 解:∵点O是对角线AC的中点,E是AB上的点沿CE折叠后,点B恰好与点O重合,
∴AC=2OC=2BC,∠B=90°,∠ACE=∠BCE,
∴sin∠BAC=$\frac{BC}{AC}$=$\frac{6}{12}=\frac{1}{2}$,
∴∠BAC=30°,
∴∠ACB=90°-∠BAC=60°,
∴∠BCE=30°,
∴CE=$\frac{BC}{cos30°}$=$\frac{6}{\frac{\sqrt{3}}{2}}$=4$\sqrt{3}$.
故选B.
点评 此题考查了折叠的性质、矩形的性质以及三角函数的性质.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
17.计算(-3)×2的结果是( )
| A. | 5 | B. | -5 | C. | 6 | D. | -6 |
18.化简:$\frac{x-4}{{x}^{2}-9}$÷(1-$\frac{1}{x-3}$)的结果是( )
| A. | x-4 | B. | x+3 | C. | $\frac{1}{x-3}$ | D. | $\frac{1}{x+3}$ |
15.已知一个反比例函数的图象经过点A(3,-4),那么不在这个函数图象上的点是( )
| A. | (-3,-4) | B. | (-3,4) | C. | (2,-6) | D. | ($\frac{\sqrt{2}}{2}$,-12$\sqrt{2}$) |
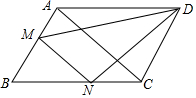 如图,在平行四边形ABCD中,MN∥AC,求证:S△ADM=S△CDN.
如图,在平行四边形ABCD中,MN∥AC,求证:S△ADM=S△CDN.