题目内容
15.已知一个反比例函数的图象经过点A(3,-4),那么不在这个函数图象上的点是( )| A. | (-3,-4) | B. | (-3,4) | C. | (2,-6) | D. | ($\frac{\sqrt{2}}{2}$,-12$\sqrt{2}$) |
分析 只需把所给点的横纵坐标相乘,结果是-12的,就在此函数图象上.
解答 解:设反比例函数的解析式为:y=$\frac{k}{x}$(k≠0).
∵反比例函数的图象经过点(3,-4),
∴k=3×(-4)=-12.
∴只需把各点横纵坐标相乘,结果为-12的点在函数图象上,
四个选项中只有A不符合.
故选:A.
点评 本题主要考查反比例函数图象上点的坐标特征,所有在反比例函数上的点的横纵坐标的积应等于比例系数.

练习册系列答案
相关题目
5.蜀山区三月中旬每天平均空气质量指数(AQI)分别为:118,96,60,82,56,69,86,112,108,94,为了描述这十天空气质量的变化情况,最适合用的统计图是( )
| A. | 折线统计图 | B. | 频数分布直方图 | C. | 条形统计图 | D. | 扇形统计图 |
6.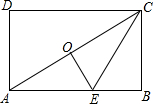 如图,已知矩形ABCD中,点E在AB上,点O是对角线AC的中点,沿CE折叠后,点B恰好与点O重合,若BC=6,则折痕CE的长为( )
如图,已知矩形ABCD中,点E在AB上,点O是对角线AC的中点,沿CE折叠后,点B恰好与点O重合,若BC=6,则折痕CE的长为( )
 如图,已知矩形ABCD中,点E在AB上,点O是对角线AC的中点,沿CE折叠后,点B恰好与点O重合,若BC=6,则折痕CE的长为( )
如图,已知矩形ABCD中,点E在AB上,点O是对角线AC的中点,沿CE折叠后,点B恰好与点O重合,若BC=6,则折痕CE的长为( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8 | D. | 10 |
3.下列图形中既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.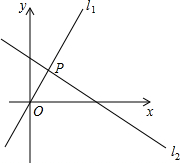 如图,直线l1过原点,直线l2解析式为y=-$\frac{\sqrt{3}}{3}$x+2,且直线l1和l2互相垂直,那么直线l1解析式为( )
如图,直线l1过原点,直线l2解析式为y=-$\frac{\sqrt{3}}{3}$x+2,且直线l1和l2互相垂直,那么直线l1解析式为( )
 如图,直线l1过原点,直线l2解析式为y=-$\frac{\sqrt{3}}{3}$x+2,且直线l1和l2互相垂直,那么直线l1解析式为( )
如图,直线l1过原点,直线l2解析式为y=-$\frac{\sqrt{3}}{3}$x+2,且直线l1和l2互相垂直,那么直线l1解析式为( )| A. | y=$\frac{1}{3}$x | B. | y=$\frac{\sqrt{3}}{3}$x | C. | y=$\frac{\sqrt{3}}{2}$x | D. | y=$\sqrt{3}$x |
7.如图,将正方形ABCD的四个角向内折起,恰好拼成一个无缝无重叠的四边形EFGH,再将四边形EFGH的一个角向内折起,使点F恰好和EG的中点重合,折痕为IJ,若点H到IJ的距离HK=9cm,则边AB的长是( )


| A. | 16cm | B. | 12cm | C. | 9cm | D. | 6$\sqrt{2}$cm |
6.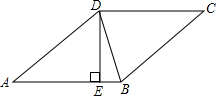 如图所示,菱形ABCD的周长为20 cm,DE⊥AB,垂足为E,sinA=$\frac{3}{5}$,则下列结论错误的是( )
如图所示,菱形ABCD的周长为20 cm,DE⊥AB,垂足为E,sinA=$\frac{3}{5}$,则下列结论错误的是( )
 如图所示,菱形ABCD的周长为20 cm,DE⊥AB,垂足为E,sinA=$\frac{3}{5}$,则下列结论错误的是( )
如图所示,菱形ABCD的周长为20 cm,DE⊥AB,垂足为E,sinA=$\frac{3}{5}$,则下列结论错误的是( )| A. | DE=3 cm | B. | BE=1 cm | ||
| C. | 菱形的面积为15 cm2 | D. | BD=2$\sqrt{10}{cm}$ |