题目内容
18. 如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.
如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.(1)当点D运动到AB的中点时,直接写出AE的长;
(2)当DF⊥AB时,求AD的长;
(3)在运动过程中线段GE的长是否发生变化?如果不变,求出线段GE的长;如果发生改变请说明理由.
分析 (1)由点D运动到AB的中点时,于是得到AD=$\frac{1}{2}$AB=3,根据等边三角形的性质得到∠A=60°,求得∠ADE=30°,根据直角三角形的性质即可得到结论;
(2)由点D、F同时运动且速度相同,得到AD=CF,求出∠AGD=∠CGF=30°,∠F=30°,于是得到CF=CG=AD,设AD=CG=CF=x,则AG=2x,列方程即可得到结论;
(3)当点D、F同时运动且速度相同时,线段GE的长度不会改变.理由如下:作FQ⊥AC,交直线AC的延长线于点Q,连接FE,DQ,由点D、F速度相同,得到AD=CF,根据等边三角形的性质得到∠A=∠ABC=∠QCF=60°,推出△ADE≌△CFQ(AAS),根据全等三角形的性质得到AE=CQ,DE=QF且DE∥QF,证得四边形DEFQ是平行四边形,根据平行四边形的性质得到GE=$\frac{1}{2}$EQ,推出GE=$\frac{1}{2}$AC,即可得到结论.
解答 解:(1)点D运动到AB的中点时,
∵AD=$\frac{1}{2}$AB=3,∠A=60°,
∵DE⊥AC,
∴∠ADE=30°,
∴AE=$\frac{1}{2}$AD=$\frac{3}{2}$;
(2)∵点D、F同时运动且速度相同,
∴AD=CF,
∵DF⊥AB,∠A=60°,
∴∠AGD=∠CGF=30°,
∵∠B=60°,
∴∠F=30°,
∴∠CGF=∠F,
∴CF=CG=AD,
设AD=CG=CF=x,则AG=2x,
∴AG+CG=2x+x=3x=6,
∴x=2,
∴AD=2;
(3)当点D、F同时运动且速度相同时,线段GE的长度不会改变.理由如下:
作FQ⊥AC,交直线AC的延长线于点Q,连接FE,DQ,
又∵DE⊥AB于E,
∴∠GQF=∠AED=90°,
∵点D、F速度相同,
∴AD=CF,
∵△ABC是等边三角形,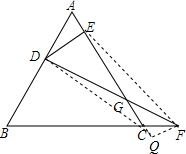
∴∠A=∠ABC=∠QCF=60°,
在△ADE和△CFQ中,
∵∠AED=∠CQF=90°,
∴∠AED=∠CQF,
在△ADE和△CQF中,
$\left\{\begin{array}{l}{∠AED=∠CQF}\\{∠A=∠QCF}\\{AD=CF}\end{array}\right.$,
∴△ADE≌△CFQ(AAS),
∴AE=CQ,DE=QF且DE∥QF,
∴四边形DEFQ是平行四边形,
∴GE=$\frac{1}{2}$EQ,
∵EC+AE=CE+CQ=AC,
∴GE=$\frac{1}{2}$AC,
又∵等边△ABC的边长为6,
∴GE=3,
∴点D、F同时运动且速度相同时,线段GE的长度不会改变.
点评 本题考查了等边三角形的性质和判定,全等三角形的性质和判定,平行线的性质,直角三角形的性质的应用,能推出两三角形全等是解此题的关键.

| A. | 2cm | B. | 4cm | C. | 6cm | D. | 不能确定 |
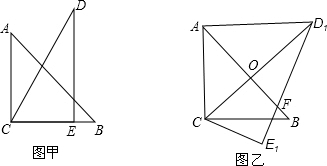
| A. | 6$\sqrt{2}$ | B. | 10 | C. | 8 | D. | $\sqrt{31}$ |
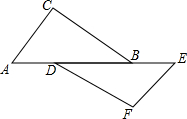 有如下命题:如图所示,点A、D、B、E在同一条直线上,则AC∥EF.判断这个命题是真命题还是假真命题,如果是真命题,请给出证明:如果是假命题,请再添加一个适当的条件使它成为一个真命题,并加以证明.
有如下命题:如图所示,点A、D、B、E在同一条直线上,则AC∥EF.判断这个命题是真命题还是假真命题,如果是真命题,请给出证明:如果是假命题,请再添加一个适当的条件使它成为一个真命题,并加以证明.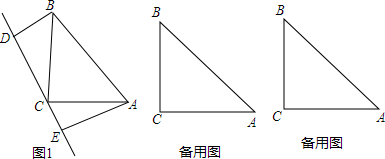
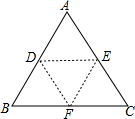 已知△ABC为等边三角形,D、E、F分别为AB边、AC边、BC边的中点,且小三角形EDF的面积为6cm2,将△ABC沿DE、EF、DF折叠后能拼成一个什么立体图形?拼成的立体图形的表面积是多少?
已知△ABC为等边三角形,D、E、F分别为AB边、AC边、BC边的中点,且小三角形EDF的面积为6cm2,将△ABC沿DE、EF、DF折叠后能拼成一个什么立体图形?拼成的立体图形的表面积是多少?