题目内容
5.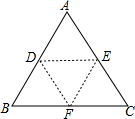 已知△ABC为等边三角形,D、E、F分别为AB边、AC边、BC边的中点,且小三角形EDF的面积为6cm2,将△ABC沿DE、EF、DF折叠后能拼成一个什么立体图形?拼成的立体图形的表面积是多少?
已知△ABC为等边三角形,D、E、F分别为AB边、AC边、BC边的中点,且小三角形EDF的面积为6cm2,将△ABC沿DE、EF、DF折叠后能拼成一个什么立体图形?拼成的立体图形的表面积是多少?
分析 根据折叠可知,将△ABC沿DE、EF、DF折叠后能拼成一个三棱锥,拼成的立体图形的表面积是小三角形EDF的面积的4倍.
解答 解:由折叠可知,将△ABC沿DE、EF、DF折叠后能拼成一个三棱锥;
∵△ABC为等边三角形,D、E、F分别为AB边、AC边、BC边的中点,
∴△ADE≌△BDF≌△CFE≌△DEF,
∴拼成的立体图形的表面积是三角形EDF的面积的4倍,
∴拼成的立体图形的表面积是6×4=24cm2.
点评 本题考查了图形的翻折变换,解决本题的根据是根据△ABC为等边三角形,D、E、F分别为AB边、AC边、BC边的中点,得到△ADE≌△BDF≌△CFE≌△DEF.

练习册系列答案
相关题目
13.周长为12的矩形窗户,当面积最大时,其一边长为( )
| A. | 3 | B. | 6 | C. | 2$\sqrt{3}$ | D. | $\sqrt{6}$ |
 如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.
如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.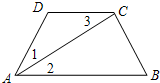 如图已知∠1=∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由.
如图已知∠1=∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由. 一座抛物线型拱桥如图所示,桥下水面宽度是6m,拱高是3m,当水面上升1m后,水面的宽度是多少?(结果精确到0.1m)
一座抛物线型拱桥如图所示,桥下水面宽度是6m,拱高是3m,当水面上升1m后,水面的宽度是多少?(结果精确到0.1m) 它的余角的度数是( )
它的余角的度数是( )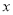 米,当
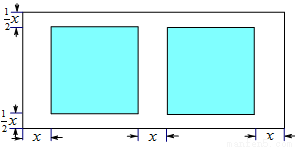
米,当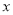 为何值时,花圃的面积之和为72米
为何值时,花圃的面积之和为72米 ?
?
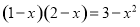 化成一般形式
化成一般形式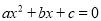 (a≠0),其中a、b、c 的值分别为( )
(a≠0),其中a、b、c 的值分别为( )