题目内容
13.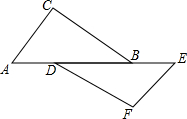 有如下命题:如图所示,点A、D、B、E在同一条直线上,则AC∥EF.判断这个命题是真命题还是假真命题,如果是真命题,请给出证明:如果是假命题,请再添加一个适当的条件使它成为一个真命题,并加以证明.
有如下命题:如图所示,点A、D、B、E在同一条直线上,则AC∥EF.判断这个命题是真命题还是假真命题,如果是真命题,请给出证明:如果是假命题,请再添加一个适当的条件使它成为一个真命题,并加以证明.
分析 此题是一道开放型的题目,答案不唯一,只要能推出∠A=∠E即可.
解答 点A、D、B、E在同一条直线上,则AC∥EF,是假命题,
条件为AC=EF,AB=DE,BC=DF,
证明:∵在△ACB和△EFD中
$\left\{\begin{array}{l}{AC=EF}\\{AB=DE}\\{BC=DF}\end{array}\right.$
∴△ACB≌△EFD(SSS),
∴∠A=∠E,
∴AC∥EF.
点评 本题考查了平行线的判定,全等三角形的性质和判定的应用,能求出∠A=∠E是解此题的关键.

练习册系列答案
相关题目
8.下列语句正确的是( )
| A. | 无限小数都是无理数 | B. | 带根号的数都是无理数 | ||
| C. | 无理数都是无限小数 | D. | 无理数的平方是无理数 |
 如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.
如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.
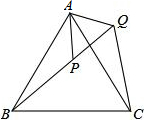 如图,△ABC是等边三角形,点P△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,求证:AP=AQ.
如图,△ABC是等边三角形,点P△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,求证:AP=AQ. 一座抛物线型拱桥如图所示,桥下水面宽度是6m,拱高是3m,当水面上升1m后,水面的宽度是多少?(结果精确到0.1m)
一座抛物线型拱桥如图所示,桥下水面宽度是6m,拱高是3m,当水面上升1m后,水面的宽度是多少?(结果精确到0.1m)