题目内容
6.已知等腰三角形ABC的两个底角∠ABC=∠ACB,且一腰AC上的高BD与另一腰AB的夹角为38°.则这个等腰三角形的底角度数为64°或26°.分析 分两种情况讨论:①若∠A<90°;②若∠A>90°;先求出顶角∠BAC,即可求出底角的度数.
解答  解:∵AB=AC,
解:∵AB=AC,
∴∠ABC=∠C,
如图1,∠ABD=38°,
∴∠A=52°,
∴∠ABC=∠C=$\frac{180°-∠A}{2}$=64°;
如图2,∠ABD=38°,
∴∠BAD=52°,
∴∠ABC=∠C=$\frac{1}{2}$∠BAD=26°.
∴这个等腰三角形的底角为:64°或26°.
故答案为:64°或26°.
点评 本题考查了等腰三角形的性质以及余角和邻补角的定义;注意分类讨论方法的运用,避免漏解.

练习册系列答案
相关题目
16.一个数的3倍比它的2倍多10,若设这个数为x,可得到方程( )
| A. | 3x-2x=10 | B. | 3x+2x=10 | C. | 3x=2×10 | D. | 3x=2x-10 |
17. 如图,点A、B、C都在⊙O上,若∠BAO=40°,则∠C的度数为( )
如图,点A、B、C都在⊙O上,若∠BAO=40°,则∠C的度数为( )
 如图,点A、B、C都在⊙O上,若∠BAO=40°,则∠C的度数为( )
如图,点A、B、C都在⊙O上,若∠BAO=40°,则∠C的度数为( )| A. | 40° | B. | 50° | C. | 80° | D. | 100° |
13.周长为12的矩形窗户,当面积最大时,其一边长为( )
| A. | 3 | B. | 6 | C. | 2$\sqrt{3}$ | D. | $\sqrt{6}$ |
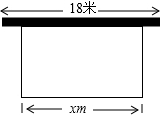 学校准备在图书馆后面的场地边建一个矩形自行车棚,一边利用图书馆的后墙,(已知后墙长18米),另三边利用总长为25米的铁围栏围成.
学校准备在图书馆后面的场地边建一个矩形自行车棚,一边利用图书馆的后墙,(已知后墙长18米),另三边利用总长为25米的铁围栏围成. 如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.
如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.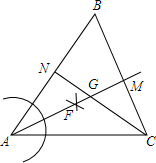 如图,在△ABC中,∠B=60°.以点A为圆心,任意长为半径画弧分别交AB、AC于点D、E,分别以点D、E为圆心,以大于$\frac{1}{2}$DE长为半径画弧,两弧相交于点F,作射线AF与BC相交于点M;
如图,在△ABC中,∠B=60°.以点A为圆心,任意长为半径画弧分别交AB、AC于点D、E,分别以点D、E为圆心,以大于$\frac{1}{2}$DE长为半径画弧,两弧相交于点F,作射线AF与BC相交于点M;