题目内容
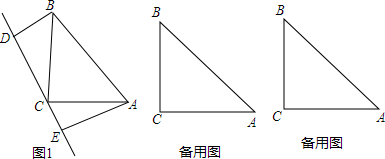
7.已知△ABC中,∠ACB=90°,AC=BC,直线CD经过直角顶点C,分别过点A、点B作CD的垂线,垂足分别为E,D(1)如图1,当直线CD与线段AB不相交时,若AE=4.8,BD=1.7,求DE的长;
(2)直线CD与线段AB相交时,题中的其他条件不变,请你先在备用图中画出图形,再限据(1)的解题经验,提出一个更一般的问题,并解决之.
分析 (1)根据已知条件得到∠AEC=∠BDC=90°,由余角的性质得到∠BCD=∠EAC,推出△BDC≌△CEA,根据全等三角形的性质得到CD=AE=4.8,CE=BD=1.7,于是得到DE=4.8+1.7=6.5;
(2)根据已知条件得到∠AEC=∠BDC=90°,由余角的性质得到∠BCD=∠EAC,推出△BDC≌△CEA,根据全等三角形的性质得到CD=AE=4.8,CE=BD=1.7,于是得到DE=CD-CE=4.8-1.7=3.1.
解答 解:(1)∵∠ACB=90°,AE⊥DE,BD⊥DE,
∴∠AEC=∠BDC=90°,
∴∠BCD=∠EAC,
在△BDC与△CEA中,
$\left\{\begin{array}{l}{∠BCD=∠EAC}\\{∠BDC=∠AEC}\\{AC=BC}\end{array}\right.$,
∴△BDC≌△CEA,
∴CD=AE=4.8,CE=BD=1.7,
∴DE=4.8+1.7=6.5;
(2)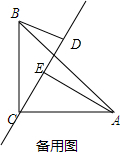 ∵∠ACB=90°,AE⊥DE,BD⊥DE,
∵∠ACB=90°,AE⊥DE,BD⊥DE,
∴∠AEC=∠BDC=90°,
∴∠BCD=∠EAC,
在△BDC与△CEA中,
$\left\{\begin{array}{l}{∠BCD=∠EAC}\\{∠BDC=∠AEC}\\{AC=BC}\end{array}\right.$,
∴△BDC≌△CEA,
∴CD=AE=4.8,CE=BD=1.7,
∴DE=4.8+1.7=6.5;
∴DE=CD-CE=4.8-1.7=3.1.
点评 本题考查了全等三角形的判定和性质,余角的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
 如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.
如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.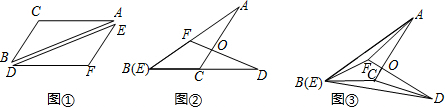
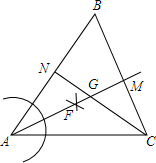 如图,在△ABC中,∠B=60°.以点A为圆心,任意长为半径画弧分别交AB、AC于点D、E,分别以点D、E为圆心,以大于$\frac{1}{2}$DE长为半径画弧,两弧相交于点F,作射线AF与BC相交于点M;
如图,在△ABC中,∠B=60°.以点A为圆心,任意长为半径画弧分别交AB、AC于点D、E,分别以点D、E为圆心,以大于$\frac{1}{2}$DE长为半径画弧,两弧相交于点F,作射线AF与BC相交于点M;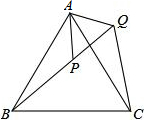 如图,△ABC是等边三角形,点P△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,求证:AP=AQ.
如图,△ABC是等边三角形,点P△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,求证:AP=AQ.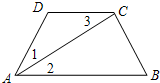 如图已知∠1=∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由.
如图已知∠1=∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由.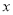 米,当
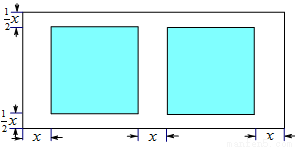
米,当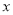 为何值时,花圃的面积之和为72米
为何值时,花圃的面积之和为72米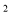 ?
?