题目内容
4.把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12,DC=14,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与 CD1交于点O,则线段AD1的长为( )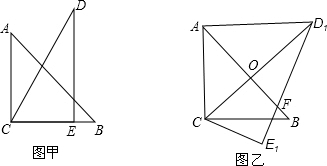
| A. | 6$\sqrt{2}$ | B. | 10 | C. | 8 | D. | $\sqrt{31}$ |
分析 先求出∠ACD=30°,再根据旋转角求出∠ACD1=45°,然后判断出△ACO是等腰直角三角形,再根据等腰直角三角形的性质求出AO、CO,AB⊥CO,再求出OD1然后利用勾股定理列式计算即可得解.
解答 解:∵∠ACB=∠DEC=90°,∠D=30°,
∴∠DCE=90°-30°=60°,
∴∠ACD=90°-60°=30°,
∵旋转角为15°,
∴∠ACD1=30°+15°=45°,
又∵∠A=45°,
∴△ACO是等腰直角三角形,
∴AO=CO=$\frac{1}{2}$AB=$\frac{1}{2}$×12=6,AB⊥CO,
∵DC=14,
∴D1C=DC=14,
∴D1O=14-6=8,
在Rt△AOD1中,AD1=$\sqrt{A{D}^{2}+{D}_{1}{O}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
故选:B.
点评 本题考查了旋转的性质,等腰直角三角形的判定与性质,勾股定理的应用,根据等腰直角三角形的性质判断出AB⊥CO是解题的关键,也是本题的难点.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
17. 如图,点A、B、C都在⊙O上,若∠BAO=40°,则∠C的度数为( )
如图,点A、B、C都在⊙O上,若∠BAO=40°,则∠C的度数为( )
 如图,点A、B、C都在⊙O上,若∠BAO=40°,则∠C的度数为( )
如图,点A、B、C都在⊙O上,若∠BAO=40°,则∠C的度数为( )| A. | 40° | B. | 50° | C. | 80° | D. | 100° |
13.周长为12的矩形窗户,当面积最大时,其一边长为( )
| A. | 3 | B. | 6 | C. | 2$\sqrt{3}$ | D. | $\sqrt{6}$ |
 如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.
如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.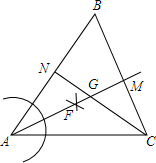 如图,在△ABC中,∠B=60°.以点A为圆心,任意长为半径画弧分别交AB、AC于点D、E,分别以点D、E为圆心,以大于$\frac{1}{2}$DE长为半径画弧,两弧相交于点F,作射线AF与BC相交于点M;
如图,在△ABC中,∠B=60°.以点A为圆心,任意长为半径画弧分别交AB、AC于点D、E,分别以点D、E为圆心,以大于$\frac{1}{2}$DE长为半径画弧,两弧相交于点F,作射线AF与BC相交于点M;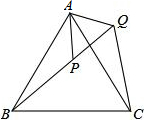 如图,△ABC是等边三角形,点P△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,求证:AP=AQ.
如图,△ABC是等边三角形,点P△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,求证:AP=AQ.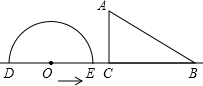 如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以1cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0(s)时,半圆O在△ABC的左侧,OC=8cm.(提示:直角三角形中,30度所对的直角边是斜边的一半,反之成立)
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以1cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0(s)时,半圆O在△ABC的左侧,OC=8cm.(提示:直角三角形中,30度所对的直角边是斜边的一半,反之成立)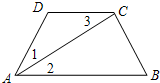 如图已知∠1=∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由.
如图已知∠1=∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由.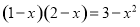 化成一般形式
化成一般形式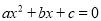 (a≠0),其中a、b、c 的值分别为( )
(a≠0),其中a、b、c 的值分别为( )