题目内容
18．已知关于x的一元二次方程x2+$\sqrt{k-1}$x-2=0有两个不相等的实数根，则k的取值范围是（ ）| A． | k＞-7 | B． | k≥-7 | C． | k≥0 | D． | k≥1 |
分析 根据二次根号下非负结合根的判别式△=k+7＞0，即可得出结论．
解答 解：∵方程x2+$\sqrt{k-1}$x-2=0有两个不相等的实数根，
∴△=$（\sqrt{k-1}）^{2}$-4×1×（-2）=k+7＞0，k-1≥0，
解得：k≥1．
故选D．
点评 本题考查了根的判别式以及二次根号下非负，熟练掌握“当△＞0时，方程有两个不相等的实数根”是解题的关键．
练习册系列答案
相关题目
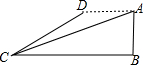如图，飞机的高度AB=1000千米，从飞机上测得地面着陆点C的俯角为18°，飞机水平飞行一段距离后，到达D点，此时测得地面着陆点C的俯角为30°，求飞机飞行的距离AD的长（参考数据：$\sqrt{3}$≈1.73，$\sqrt{2}$≈1.41，tan18°≈0.32）
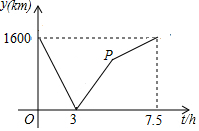A、B两城由笔直的铁路连接，动车甲从A向B匀速前行，同时动车乙从B向A匀速前行，到达目的地时停止，其中动车乙速度较快，设甲乙两车相距y（km），甲行驶的时间为t（h），y关于t的函数图象如图所示．
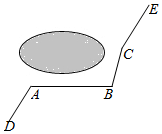如图所示，一条公路修到湖边时，为了保护生态环境，需拐弯绕湖而过，如果图中的拐角∠A=150°，∠B=120°，三次拐弯后的道路CE与原来公路DA平行，试求出∠C的度数．