题目内容
6.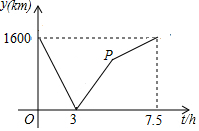 A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示.
A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示.(1)填空:动车甲的速度为$\frac{640}{3}$(km/h),动车乙的速度为320(km/h);
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)两车何时相距1200km?
分析 (1)根据图中信息即可得到两车的速度;
(2)根据题意和图形即可得到点P的坐标以及点P表示的实际意义;
(3)根据题意,利用分类讨论的数学思想可以解答本题.
解答 解:(1)动车甲的速度=$\frac{1600}{7.5}$=$\frac{640}{3}$km/h,动车乙的速度,=$\frac{1600-\frac{640}{3}×3}{3}$=320km/h;
(2)由题意可得,
点P的横坐标为:1600÷320=5,纵坐标为:$\frac{640}{3}×5$=$\frac{3200}{3}$,
即点P的坐标为(5,$\frac{3200}{3}$),
该点坐标表示的实际意义是此时动车乙到达目的地,动车甲鱼动车乙的距离为$\frac{3200}{3}$km;
(3)由题意可得,
当相遇前相遇1200km,此时的时间为:$\frac{1600-1200}{\frac{640}{3}+320}$=0.75h,
当相遇后相遇1200km,由(2)知,当动车乙到达目的地时两车相距$\frac{3200}{3}<1200$,
故此时的时间为:$\frac{1200}{\frac{640}{3}}=\frac{45}{8}$h,
即两车在0.75h和$\frac{45}{8}$h相距1200km.
点评 本题考查了一次函数应用中的相遇问题,解题的关键是明确题意,利用数形结合的思想和分类讨论的数学思想解答.

练习册系列答案
相关题目
14. 如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )
如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )
 如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )
如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )| A. | 24 | B. | 30 | C. | 18 | D. | 14.4 |
18.已知关于x的一元二次方程x2+$\sqrt{k-1}$x-2=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>-7 | B. | k≥-7 | C. | k≥0 | D. | k≥1 |
 如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是3$\sqrt{2}$cm.
如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是3$\sqrt{2}$cm. 如图,在Rt△ABC中,∠C=90°,CA=CB=4,将△ABC翻折,使得点B与边AC的中点M重合,如果折痕与边AB的交点为E,那么BE的长为$\frac{5\sqrt{2}}{3}$.
如图,在Rt△ABC中,∠C=90°,CA=CB=4,将△ABC翻折,使得点B与边AC的中点M重合,如果折痕与边AB的交点为E,那么BE的长为$\frac{5\sqrt{2}}{3}$.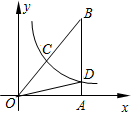 如图,已知反比例函数y=$\frac{k}{x}$(k>0)的图象经过Rt△OAB斜边OB的中点C,且与直角边AB相交于点D,若B的坐标为(4,6),则△BOD的面积为9.
如图,已知反比例函数y=$\frac{k}{x}$(k>0)的图象经过Rt△OAB斜边OB的中点C,且与直角边AB相交于点D,若B的坐标为(4,6),则△BOD的面积为9.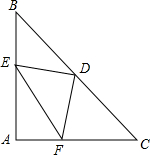 如图,在△ABC中,AB=AC,∠A=90°,点D是BC边的中点,点E,F分别在AB,AC上.且DE⊥DF.
如图,在△ABC中,AB=AC,∠A=90°,点D是BC边的中点,点E,F分别在AB,AC上.且DE⊥DF. 如图所示为一个正方体截去两个角后的立体图形,如果照这样截取正方体的八个角,则新的几何体的棱有多少条?请说明你的理由.
如图所示为一个正方体截去两个角后的立体图形,如果照这样截取正方体的八个角,则新的几何体的棱有多少条?请说明你的理由.