��Ŀ����
7����ͼ1��ֱ��y=$\frac{3}{4}$x+3��x�ᡢy��ֱ��ڵ�A��B������P�ӵ�A��������ÿ��1����λ���ٶ���AB���յ�B�˶���ͬʱ����Q�ӵ�O��������ÿ��0.8����λ���ٶ���OA���յ�A�˶�������Q��ֱ��AB��ƽ���߽�y���ڵ�C�����˶�ʱ��Ϊt��0��t��5���룮��1�������˶������У��ı���APCQ�Ǻ���������ı��Σ���֤����Ľ��ۣ�
��2����tΪ��ֵʱ���ı���APCQ�����Σ�
��3����ͼ2����D�ڶ���Q�Ҳ��x���ϣ���ʼ������QD=1����M��ֱ��AB�ϣ��������Ϊ-3���ʵ�tΪ��ֵʱ���ı���MQDB���ܳ���С����Сֵ�Ƕ��٣�
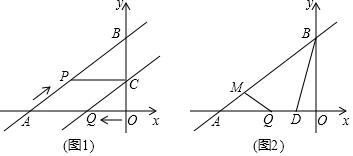
���� ��1���ɡ�ABO�ס�QCO���Ƴ�$\frac{AB}{QC}$=$\frac{AO}{QO}$���Ƴ�$\frac{5}{QC}$=$\frac{4}{0.8t}$���Ƴ�QC=t����AP=t���ɵ�AP=QC��AP��QC������֤����
��2�����ı���ʽAPCQ������ʱ������AP=AQ����ɵõ�����t�ķ��̣������t��ֵ��
��3����ͼ2�У�������M��-3��$\frac{3}{4}$��������M����ƽ��1����λ�õ�M�䣨-2��$\frac{3}{4}$��������M�����OA�ĶԳƵ�M�壨-2��-$\frac{3}{4}$��������BM�彻OA��D����ʱ�ı���MQDB���ܳ���̣����ֱ��BM��Ľ���ʽ���ɵõ�D���꣬�ɴ˼��ɽ�����⣮
��� �⣺��1�����ۣ��ı���APCQ��ƽ���ı��Σ��������£�
��ֱ��y=$\frac{3}{4}$x+3��x�ᡢy��ֱ��ڵ�A��B��
��A��-4��0����B��0��3����
��OA=4��OB=3��AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5��
��QC��AB��
���ABO�ס�QCO��
��$\frac{AB}{QC}$=$\frac{AO}{QO}$��
��$\frac{5}{QC}$=$\frac{4}{0.8t}$��
��QC=t��
��AP=t��
��AP=QC����AP��QC��
���ı���APCQ��ƽ���ı��Σ�
��2�����ı���APCQ��ƽ���ı��Σ�
�൱AP=AQʱ���ı���APCQ�����Σ�
��t=4-0.8t��
��t=$\frac{20}{9}$s��
�൱tΪ$\frac{20}{9}$sʱ���ı���APCQ�����Σ�
��3����ͼ2�У�������M��-3��$\frac{3}{4}$����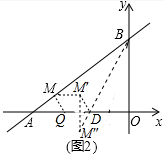
����M����ƽ��1����λ�õ�M�䣨-2��$\frac{3}{4}$��������M�����OA�ĶԳƵ�M�壨-2��-$\frac{3}{4}$��������BM�彻OA��D����ʱ�ı���MQDB���ܳ���̣�
��ֱ��BM��Ľ���ʽΪy=kx+b������$\left\{\begin{array}{l}{b=3}\\{-2k+b=-\frac{3}{4}}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=\frac{15}{8}}\\{b=3}\end{array}\right.$��
��ֱ��BM��Ľ���ʽΪy=$\frac{15}{8}$x+3����y=0�õ�x=-$\frac{8}{5}$��
��D��-$\frac{8}{5}$��0����
��OQ=1+$\frac{8}{5}$=$\frac{13}{5}$��
��t=$\frac{13}{5}$��0.8=$\frac{13}{4}$s��
�ı���MQDB���ܳ�����Сֵ=MQ+QD+DB+BM
=DQ+DM��+BD+BM
=QD+M��D+DB+BM
=QD+BM��+BM
=1+$\sqrt{{2}^{2}+��3+\frac{3}{4}��^{2}}$+$\sqrt{{3}^{2}+��3-\frac{3}{4}��^{2}}$
=1+$\frac{17}{4}$+$\frac{15}{4}$=9��
���� ���⿼��һ�κ����ۺ��⡢ƽ���ı��ε��ж������ʡ����ε��ж������ʡ����ɶ��������������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����öԳơ�ƽ�Ƶ�֪ʶ���������⣬�����п�ѹ���⣮

| A�� | k��-7 | B�� | k��-7 | C�� | k��0 | D�� | k��1 |

| A�� | 2018 | B�� | 2017 | C�� | 2016 | D�� | 2015 |
| A�� | ��24 | B�� | ��24 | C�� | ��4 | D�� | ��4 |
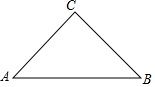 ��ͼ����Rt��ABC�У���C=90�㣬CA=CB=4������ABC���ۣ�ʹ�õ�B���AC���е�M�غϣ�����ۺ����AB�Ľ���ΪE����ôBE�ij�Ϊ$\frac{5\sqrt{2}}{3}$��
��ͼ����Rt��ABC�У���C=90�㣬CA=CB=4������ABC���ۣ�ʹ�õ�B���AC���е�M�غϣ�����ۺ����AB�Ľ���ΪE����ôBE�ij�Ϊ$\frac{5\sqrt{2}}{3}$��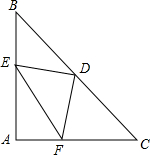 ��ͼ���ڡ�ABC�У�AB=AC����A=90�㣬��D��BC�ߵ��е㣬��E��F�ֱ���AB��AC�ϣ���DE��DF��
��ͼ���ڡ�ABC�У�AB=AC����A=90�㣬��D��BC�ߵ��е㣬��E��F�ֱ���AB��AC�ϣ���DE��DF�� ��ͼ��ʾΪһ���������ȥ�����Ǻ������ͼ�Σ������������ȡ������İ˸��ǣ����µļ���������ж���������˵��������ɣ�
��ͼ��ʾΪһ���������ȥ�����Ǻ������ͼ�Σ������������ȡ������İ˸��ǣ����µļ���������ж���������˵��������ɣ�