题目内容
10. 已知:如图,在平行四边形ABCD中,延长CB至E,延长AD至F,使得BE=DF,连接EF与对角线AC交于点O.求证:OE=OF.
已知:如图,在平行四边形ABCD中,延长CB至E,延长AD至F,使得BE=DF,连接EF与对角线AC交于点O.求证:OE=OF.
分析 由平行四边形的性质得出AB∥CD,AD=BC,证出AF=CE,∠E=∠F,∠AOF=∠EOC,由ASA证明△AOF≌△COE,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC,
∵BE=DF,
∴BC+BE=AD+DF,即CE=AF,
∵AD∥CB,
∴AF∥CE,
∴∠E=∠F,∠OAE=∠OCF,
在△AOF和△COE中,$\left\{\begin{array}{l}{∠F=∠E}\\{∠AOF=∠EOC}\\{AF=CE}\end{array}\right.$,
∴△AOF≌△COE(ASA),
∴OE=OF.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质、平行线的性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
5.一个不透明的盒子中装有3个红球,2个黄球和1个白球,这些球除了颜色外无其他差别,从中随机摸出一个小球,恰好是红球的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
15.若一个多边形的内角和等于外角和,则这个多边形的边数是( )
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
3.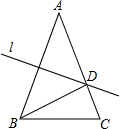 如图,AB=AC=5cm,BC=3cm,直线l是AB的垂直平分线,AC与l相交于点D,则△BDC的周长是( )
如图,AB=AC=5cm,BC=3cm,直线l是AB的垂直平分线,AC与l相交于点D,则△BDC的周长是( )
 如图,AB=AC=5cm,BC=3cm,直线l是AB的垂直平分线,AC与l相交于点D,则△BDC的周长是( )
如图,AB=AC=5cm,BC=3cm,直线l是AB的垂直平分线,AC与l相交于点D,则△BDC的周长是( )| A. | 10 cm | B. | 11 cm | C. | 6 cm | D. | 8 cm |
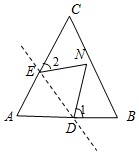 如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平,使点A与点N重合.
如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平,使点A与点N重合. 如图所示,在长为32m,宽为20m的矩形耕地上,修筑同样宽的三条道路(互相垂直),把耕地分成大小不等的六块试验田,要使试验田的面积为570m2,道路的宽度应为多少?
如图所示,在长为32m,宽为20m的矩形耕地上,修筑同样宽的三条道路(互相垂直),把耕地分成大小不等的六块试验田,要使试验田的面积为570m2,道路的宽度应为多少?