题目内容
5.阅读材料我们知道:若分式$\frac{(x-1)(x-2)}{x}$的值为零,则x=1或x=2
又因为$\frac{(x-1)(x-2)}{x}$=$\frac{{x}^{2}-(1+2)x+1×2}{x}$=$\frac{{x}^{2}+1×2-(1+2)x}{x}$=x+$\frac{1×2}{x}$-(1+2)
所以$\frac{(x-1)(x-2)}{x}$=0可化为:x+$\frac{1×2}{x}$-(1+2)=0,则x+$\frac{1×2}{x}$=1+2
所以关于x的方程x+$\frac{1×2}{x}$=1+2有两个解,分别为x=1或x=2.
类似的有:对于不相等且非零实数a、b,关于x的方程x+$\frac{ab}{x}$=a+b有两个解分别为x1=a,x2=b.应用材料中的结论解答下列问题:
(1)方程x+$\frac{8}{x}$=6的两个解分别为x1=2,x2=4;
(2)关于x的方程x+$\frac{m-n}{mnx}$=$\frac{m+4mn-n}{2mn}$的两个解分别为x1、x2(x1<x2),若x1与x2互为倒数,则x1=$\frac{1}{2}$,x2=2;
(3)关于x的方程2x+$\frac{{n}^{2}+2n-3}{2x-1}$=2n+3的两个解分别为x1、x2(x1<x2),求$\frac{{x}_{2}-2}{2{x}_{1}}$的值.
分析 (1)方程变形后,利用题中的结论确定出较大的解即可;
(2)方程变形后,根据利用题中的结论,以及x1与x2互为倒数,确定出x1与x2的值即可;
(3)方程变形后,根据利用题中的结论表示出为x1、x2,代入原式计算即可得到结果.
解答 解:(1)∵2×4=8,2+4=6,
∴方程x+$\frac{8}{x}$=6的两个解分别为x1=2,x2=4.
故答案为:x1=2,x2=4.
(2)方程变形得:x+$\frac{\frac{m-n}{2mn}×2}{x}$=$\frac{m-n}{2mn}$+2,
由题中的结论得:方程有一根为2,另一根为$\frac{1}{2}$,
则x1=$\frac{1}{2}$,x2=2;
故答案为:$\frac{1}{2}$;2
(3)方程整理得:2x-1+$\frac{(n-1)(n+3)}{2x-1}$=n-1+n+3,
得2x-1=n-1或2x-1=n+3,
可得x1=$\frac{n}{2}$,x2=$\frac{n+4}{2}$,
则原式=$\frac{\frac{n+4}{2}-2}{2•\frac{n}{2}}$=$\frac{1}{2}$.
点评 此题考查了分式方程的解,弄清题中的规律是解本题的关键.

练习册系列答案
相关题目
17. 如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )
如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )
 如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )
如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )| A. | $\widehat{BC}$=$\frac{1}{2}$$\widehat{AC}$ | B. | $\widehat{BC}$=$\frac{1}{3}$$\widehat{AC}$ | C. | $\widehat{BC}$=$\widehat{AC}$ | D. | 不能确定 |
14.若关于x的分式方程$\frac{m}{x-3}=\frac{2x}{3-x}+1$有增根,则这个增根是( )
| A. | x=3 | B. | x=1 | C. | x=-1 | D. | x=-3 |
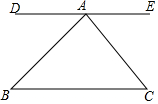 如图,直线DE经过点A,DE∥BC,∠B=45°,∠C=50°,
如图,直线DE经过点A,DE∥BC,∠B=45°,∠C=50°, 已知:如图,在平行四边形ABCD中,延长CB至E,延长AD至F,使得BE=DF,连接EF与对角线AC交于点O.求证:OE=OF.
已知:如图,在平行四边形ABCD中,延长CB至E,延长AD至F,使得BE=DF,连接EF与对角线AC交于点O.求证:OE=OF.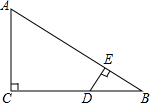 已知:如图,在△ABC中,∠C=90°,D是BC上一点,DE⊥AB于E,若AC=6,AB=10,DE=2.
已知:如图,在△ABC中,∠C=90°,D是BC上一点,DE⊥AB于E,若AC=6,AB=10,DE=2.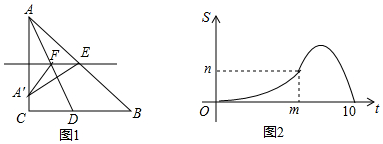
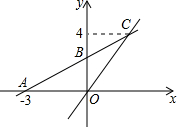 如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(-3,0),与y轴交点为B,且与正比例函数y=$\frac{4}{3}x$的图象交于点C(m,4),求m的值及点B的坐标.
如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(-3,0),与y轴交点为B,且与正比例函数y=$\frac{4}{3}x$的图象交于点C(m,4),求m的值及点B的坐标.