题目内容
2.(1)画图-连线-写依据:先分别完成以下画图(不要求尺规作图),再与判断四边形DEMN形状的相应结论连线,并写出判定依据(只将最后一步判定特殊平行四边形的依据填在横线上).
①如图1,在矩形ABEN中,D为对角线的交点,过点N画直线NP∥DE,过点E画直线EQ∥DN,NP与EQ的交点为点M,得到四边形DEMN.
②如图2,在菱形ABFG中,顺次连接四边形AB,BF,FG,GA的中点D,E,M,N,得到四边形DEMN.
(2)请从图1,图2的结论中选择一个进行证明.
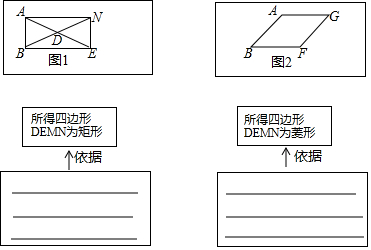
请先在以下相应方框内打勾,在证明想用结论.

证明:
分析 (1)根据题意作出图形即可;
(2)①如图4,根据平行四边形的判定定理得到四边形DEMN是平行四边形,根据矩形的想最大的DE=DN,于是得到结论;②如图6,连接AF,BG交于H根据三角形的中位线的性质得到DN∥BG,DN=$\frac{1}{2}$BG,EM∥BG,EM=$\frac{1}{2}$BG,DE∥AF,DE=$\frac{1}{2}$AF,推出四边形DEFG是平行四边形,根据菱形的性质得到AF⊥BG,求得∠2=180°-∠1=90°,于是得到结论.
解答 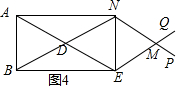 解:(1)如图4,四边形DEMN为菱形,依据:有一组邻边相等的平行四边形是菱形;
解:(1)如图4,四边形DEMN为菱形,依据:有一组邻边相等的平行四边形是菱形;
如图5,四边形DEMN为矩形,依据:由一个角等于90°的平行四边形是矩形;
(2)①如图4,∵PN∥DE,∥DN,PN,EQ的交点我M,
∴四边形DEMN是平行四边形,
∵D是矩形ABEN对角线的交点,
∴AE=BN,DE=$\frac{1}{2}$AE,DN=$\frac{1}{2}$BN,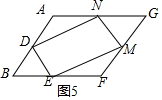
∴DE=DN,
∴四边形DEMN是菱形;
②如图6,连接AF,BG交于H,
∵D,N是AB,GA,的中点,
∴DN∥BG,DN=$\frac{1}{2}$BG,
同理:EM∥BG,EM=$\frac{1}{2}$BG,DE∥AF,DE=$\frac{1}{2}$AF,
∴DN∥EM,DN=EM,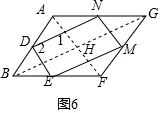
∴四边形DEFG是平行四边形,
∵四边形ABFG是 菱形,
∴AF⊥BG,
∴∠AHB=90°,
∴∠1=180°-∠AHB=90°,
∴∠2=180°-∠1=90°,
∴平行四边形DEMN是矩形.
点评 本题考查了中点四边形,矩形的判定和性质,菱形的判定和性质,三角形的中位线的性质,熟练掌握矩形和菱形的判定定理是解题的关键.

练习册系列答案
相关题目
17. 如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )
如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )
 如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )
如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )| A. | $\widehat{BC}$=$\frac{1}{2}$$\widehat{AC}$ | B. | $\widehat{BC}$=$\frac{1}{3}$$\widehat{AC}$ | C. | $\widehat{BC}$=$\widehat{AC}$ | D. | 不能确定 |
7.若关于x的一元一次方程2x+3a=1的解为x=2,则关于m的一元一次不等式3-m>a的解集为( )
| A. | m<2 | B. | m<4 | C. | m>2 | D. | m>4 |
14.若关于x的分式方程$\frac{m}{x-3}=\frac{2x}{3-x}+1$有增根,则这个增根是( )
| A. | x=3 | B. | x=1 | C. | x=-1 | D. | x=-3 |
11.下列调查中,适合采用全面调查的是( )
| A. | 调查某批次圆珠笔的使用寿命 | |
| B. | 端午节期间,食品检查部门调查市场上粽子的质量情况 | |
| C. | 调查某班46同学的视力情况 | |
| D. | 检测我地区的空气质量 |
12.下列图形中,轴对称图形的个数是( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 已知:如图,在平行四边形ABCD中,延长CB至E,延长AD至F,使得BE=DF,连接EF与对角线AC交于点O.求证:OE=OF.
已知:如图,在平行四边形ABCD中,延长CB至E,延长AD至F,使得BE=DF,连接EF与对角线AC交于点O.求证:OE=OF.