题目内容
6.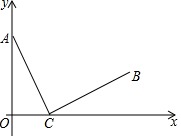 已知,点C(4,0)在x轴上,动点A(0,m)在y轴上,线段CB出线段CA绕点C顺时针旋转90°得到,如图所示,∠ACB=90°,AC=BC.
已知,点C(4,0)在x轴上,动点A(0,m)在y轴上,线段CB出线段CA绕点C顺时针旋转90°得到,如图所示,∠ACB=90°,AC=BC.(1)当m=6时,求点B的坐标;
(2)当m=-6时,求点B的坐标;
(3)若点Q(-1,0),当BQ最小时,直接写出m的值.
分析 (1)先过点B作BD⊥x轴于点D,根据AAS判定△ACO≌△CBD,根据全等三角形的对应边相等,得出BD=4,OD=10,求得点B的坐标;
(2)先过点B作BD⊥x轴于点D,根据AAS判定△ACO≌△CBD,根据全等三角形的对应边相等,得出BD=4,OD=2,求得点B的坐标;
(3)过点B作BD⊥x轴于点D,根据全等三角形的性质,求得BD=CO=4,再根据垂线段最短,得出当点D与点Q重合时,BQ最小,求得此时AO=CQ=5,即可得到m的值.
解答 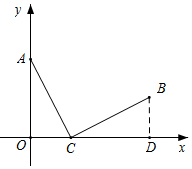 解:(1)如图所示,当m=6时,过点B作BD⊥x轴于点D,则∠CDB=∠AOC=90°,
解:(1)如图所示,当m=6时,过点B作BD⊥x轴于点D,则∠CDB=∠AOC=90°,
∵∠ACB=90°,AC=BC,
∴∠CAO+∠ACO=∠BCD+∠ACO=90°,
∴∠CAO=∠BCD,
∴△ACO≌△CBD(AAS),
∵C(4,0),A(0,6),
∴BD=CO=4,CD=AO=6,
∴OD=10,
∴此时,点B的坐标为(10,4);
(2)如图所示,当m=6时,过点B作BD⊥x轴于点D,则∠CDB=∠AOC=90°,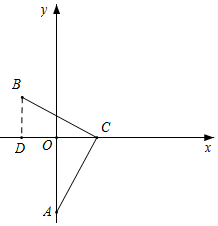
∵∠ACB=90°,AC=BC,
∴∠CAO+∠ACO=∠BCD+∠ACO=90°,
∴∠CAO=∠BCD,
∴△ACO≌△CBD(AAS),
∵C(4,0),A(0,-6),
∴BD=CO=4,CD=AO=6,
∴OD=2,
∴此时,点B的坐标为(-2,4);
(3)如图所示,过点B作BD⊥x轴于点D,则∠CDB=∠AOC=90°,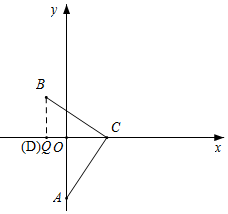
∵∠ACB=90°,AC=BC,
∴∠CAO+∠ACO=∠BCD+∠ACO=90°,
∴∠CAO=∠BCD,
∴△ACO≌△CBD(AAS),
∵C(4,0),
∴BD=CO=4,
连接BQ,则当点D与点Q重合时,BD=BQ=4,
根据垂线段最短,可知此时BQ最小,
∵Q(-1,0),C(4,0),
∴此时,AO=CQ=5,
又∵点A在y轴负半轴上,
∴m的值为-5.
点评 本题主要考查了全等三角形的判定与性质,垂线段最短的综合应用,解决问题的关键是作辅助线构造全等三角形,运用全等三角形的对应边相等进行计算求解.实际问题中涉及线路最短问题时,其理论依据应从“两点之间,线段最短”和“垂线段最短”这两个中去选择.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案| A. | 开口方向 | B. | 开口大小 | C. | 最高点的坐标 | D. | 对称轴 |
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
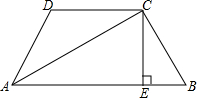 已知:四边形ABCD中,∠B+∠D=180°,AC平分∠BAD,点E在AB上,满足∠ADC-∠ABC=2∠BCE,求证:CE⊥AB.
已知:四边形ABCD中,∠B+∠D=180°,AC平分∠BAD,点E在AB上,满足∠ADC-∠ABC=2∠BCE,求证:CE⊥AB.
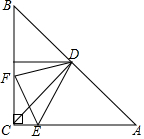 已知△ACB为等腰直角三角形,D为BA的中点,∠EDF=45°,交AC于E点,交BC于F点,连EF.
已知△ACB为等腰直角三角形,D为BA的中点,∠EDF=45°,交AC于E点,交BC于F点,连EF. 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是x=1,有以下四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是x=1,有以下四个结论: