题目内容
1.若x1、x2是一元二次方程x2+2x-6=0的两根,则x12+x22=16.分析 根据根与系数的关系得到x1+x2=-2,x1•x2=-6,再变形x12+x22得到(x1+x2)2-2x1•x2,然后利用代入计算即可.
解答 解:∵一元二次方程x2+2x-6=0的两根是x1、x2,
∴x1+x2=-2,x1•x2=-6,
∴x12+x22=(x1+x2)2-2x1•x2=(-2)2-2×(-6)=16.
故答案为:16.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.关于抛物线y=ax2和y=-ax2(a≠0),给出下列说法:
①两条抛物线都关于x轴对称;
②两条抛物线都关于原点对称;
③两条抛物线各自关于y轴对称;
④两条抛物线有公共的顶点.
其中正确的说法有( )
①两条抛物线都关于x轴对称;
②两条抛物线都关于原点对称;
③两条抛物线各自关于y轴对称;
④两条抛物线有公共的顶点.
其中正确的说法有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.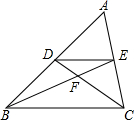 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )| A. | $\frac{DF}{FC}=\frac{AE}{AC}$ | B. | $\frac{AD}{AB}=\frac{EC}{AC}$ | C. | $\frac{AD}{DB}=\frac{DE}{BC}$ | D. | $\frac{DF}{BF}=\frac{EF}{FC}$ |
8. 如图,在△ABC中,∠ACB=90°,将△ABC绕着点A逆时针旋转得到△ADE,点C落在边AD上,连接BD.若∠DAE=α,则用含α的式子表示∠CBD的大小是( )
如图,在△ABC中,∠ACB=90°,将△ABC绕着点A逆时针旋转得到△ADE,点C落在边AD上,连接BD.若∠DAE=α,则用含α的式子表示∠CBD的大小是( )
 如图,在△ABC中,∠ACB=90°,将△ABC绕着点A逆时针旋转得到△ADE,点C落在边AD上,连接BD.若∠DAE=α,则用含α的式子表示∠CBD的大小是( )
如图,在△ABC中,∠ACB=90°,将△ABC绕着点A逆时针旋转得到△ADE,点C落在边AD上,连接BD.若∠DAE=α,则用含α的式子表示∠CBD的大小是( )| A. | α | B. | 90°-α | C. | $\frac{α}{2}$ | D. | 90$°-\frac{α}{2}$ |
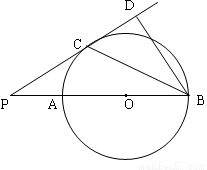
 如图,在边长为1的正方形组成的6×5方格中,点A,B都在格点上.
如图,在边长为1的正方形组成的6×5方格中,点A,B都在格点上.
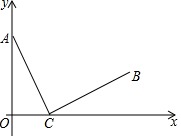 已知,点C(4,0)在x轴上,动点A(0,m)在y轴上,线段CB出线段CA绕点C顺时针旋转90°得到,如图所示,∠ACB=90°,AC=BC.
已知,点C(4,0)在x轴上,动点A(0,m)在y轴上,线段CB出线段CA绕点C顺时针旋转90°得到,如图所示,∠ACB=90°,AC=BC.