题目内容
17.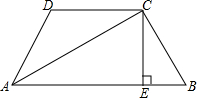 已知:四边形ABCD中,∠B+∠D=180°,AC平分∠BAD,点E在AB上,满足∠ADC-∠ABC=2∠BCE,求证:CE⊥AB.
已知:四边形ABCD中,∠B+∠D=180°,AC平分∠BAD,点E在AB上,满足∠ADC-∠ABC=2∠BCE,求证:CE⊥AB.
分析 先过C作CF垂直AD于F,根据∠B+∠ADC=180°,∠ADC-∠B=2∠BCE,得出∠ADC=90°+∠BCE,再根据三角形外角性质,得出∠ADC=90°+∠DCF,进而得到∠DCF=∠BCE,最后根据∠B=∠CDF,得出∠CFD=∠CEB=90°即可.
解答  证明:过C作CF垂直AD于F,则∠CFD=90°,
证明:过C作CF垂直AD于F,则∠CFD=90°,
∵∠B+∠ADC=180°,∠ADC-∠B=2∠BCE,
∴两式相加,可得2∠ADC=180°+2∠BCE,
即∠ADC=90°+∠BCE,①
又∵∠ADC是△CDF的外角,∠CFD=90°,
∴∠ADC=90°+∠DCF,②
由①②可得,∠DCF=∠BCE,
∵∠B+∠ADC=180°,∠CDF+∠ADC=180°,
∴∠B=∠CDF,
∴∠CFD=∠CEB=90°,
∴CE⊥AB.
点评 本题主要考查了三角形内角和定理、邻补角以及垂线的定义的综合应用,解决问题的关键是作辅助线构造直角三角形,运用角的和差关系进行推导是本题的难点.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
5.计算2x2-3x2的结果是( )
| A. | 5x2 | B. | -5x2 | C. | x2 | D. | -x2 |
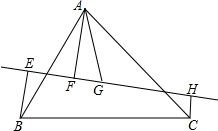 如图,直线l过△ABC的重心G,它与两边AB、AC相交,设A,B,C在l上的射影分别是F,E,H,求证:BE+CH=AF.
如图,直线l过△ABC的重心G,它与两边AB、AC相交,设A,B,C在l上的射影分别是F,E,H,求证:BE+CH=AF. 如图,在Rt△ABC中,∠ABC=90°,以AC为斜边向外作等腰Rt△ACD,连接BD.
如图,在Rt△ABC中,∠ABC=90°,以AC为斜边向外作等腰Rt△ACD,连接BD.
 如图,在边长为1的正方形组成的6×5方格中,点A,B都在格点上.
如图,在边长为1的正方形组成的6×5方格中,点A,B都在格点上.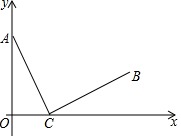 已知,点C(4,0)在x轴上,动点A(0,m)在y轴上,线段CB出线段CA绕点C顺时针旋转90°得到,如图所示,∠ACB=90°,AC=BC.
已知,点C(4,0)在x轴上,动点A(0,m)在y轴上,线段CB出线段CA绕点C顺时针旋转90°得到,如图所示,∠ACB=90°,AC=BC.