题目内容
11．
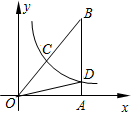如图，已知反比例函数y=$\frac{k}{x}$（k＞0）的图象经过Rt△OAB斜边OB的中点C，且与直角边AB相交于点D，若B的坐标为（4，6），则△BOD的面积为9．
分析 过点C作CE⊥OA于点E，由点C为线段OB的中点结合点B的坐标，即可求出点C的坐标，利用反比例函数系数k的几何意义即可得出S△OCE=S△ODA=3，再根据三角形的面积结合S△BOD=S△OAB-S△ODA即可求出△BOD的面积．
解答 解：过点C作CE⊥OA于点E，如图所示．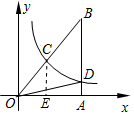
∵点C为线段OB的中点，且点B的坐标为（4，6），
∴点C（2，3）．
∵点C、D在反比例函数y=$\frac{k}{x}$的图象上，
∴S△OCE=S△ODA=$\frac{1}{2}$×2×3=3，
∴S△BOD=S△OAB-S△ODA=$\frac{1}{2}$×4×6-3=9．
故答案为：9．
点评 本题考查了反比例函数系数k的几何意义以及三角形的面积，根据反比例函数系数k的几何意义找出S△OCE=S△ODA=3是解题的关键．
练习册系列答案
相关题目
图中所示为P（14，0）和Q（2，a）两点．若PQ=13单位，求a的值．
将三角形ABC沿PQ方向平移3cm后，得到三角形A′B′C′，请你画出三角形A′B′C′．
如图，直线l1∥l2∥l3，且l1与l2的距离为1，l2与l3的距离为2，等腰△ABC的顶点分别在直线l1、l2，l3上，AB=AC，∠BAC=120°，则等腰三角形的腰长为2或$\frac{2\sqrt{39}}{3}$或$\frac{2\sqrt{57}}{3}$．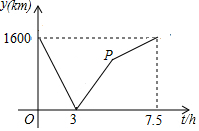
A、B两城由笔直的铁路连接，动车甲从A向B匀速前行，同时动车乙从B向A匀速前行，到达目的地时停止，其中动车乙速度较快，设甲乙两车相距y（km），甲行驶的时间为t（h），y关于t的函数图象如图所示．
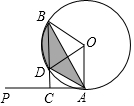如图，已知PA为⊙O的切线，A为切点，B为⊙O上一点，∠AOB=120°，过点B作BC⊥PA于点C，BC交⊙O于点D，连接AB、AD．
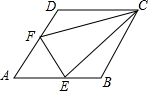如图，菱形ABCD中，∠A=60°，点E、F分别是边AB、AD上的点，且满足∠BCE=∠DCF，连接EF，当AF=$\sqrt{5}$时，求EF的长．