题目内容
15.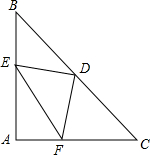 如图,在△ABC中,AB=AC,∠A=90°,点D是BC边的中点,点E,F分别在AB,AC上.且DE⊥DF.
如图,在△ABC中,AB=AC,∠A=90°,点D是BC边的中点,点E,F分别在AB,AC上.且DE⊥DF.求证:BE2+CF2=EF2.
分析 连接AD,根据等腰直角三角形的性质可得AD=BD,AD⊥BC,∠B=∠DAF=45°,再求出∠BDE=∠ADF,然后利用“角边角”证明△BDE和△ADF全等,根据全等三角形对应边相等可得BE=AF,再求出AE=CF,然后利用勾股定理列式即可得证.
解答 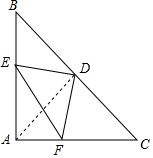 证明:如图,连接AD,
证明:如图,连接AD,
∵AB=AC,∠A=90°,点D是BC边的中点,
∴AD=BD,AD⊥BC,∠B=∠DAF=45°,
∵DE⊥DF,
∴∠ADF+∠ADE=90°,
又∵∠BDE+∠ADE=∠ADB=90°,
∴∠BDE=∠ADF,
在△BDE和△ADF中,$\left\{\begin{array}{l}{∠BDE=∠ADF}\\{AD=BD}\\{∠B=∠DAF=45°}\end{array}\right.$,
∴△BDE≌△ADF(ASA),
∴BE=AF,
∵AB=AC,
∴AB-BE=AC-AF,
即AE=CF,
在Rt△AEF中,根据勾股定理得,AF2+AE2=EF2,
∴BE2+CF2=EF2.
点评 本题考查了全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,熟练掌握三角形全等的判定方法并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
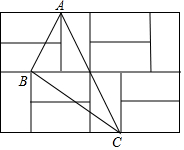 如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为4,△ABC的顶点都在格点.
如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为4,△ABC的顶点都在格点.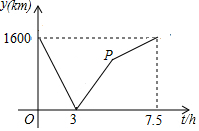 A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示.
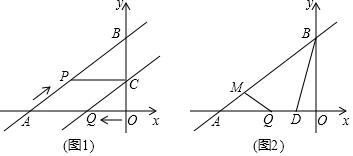
A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示.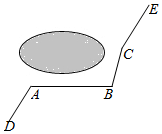 如图所示,一条公路修到湖边时,为了保护生态环境,需拐弯绕湖而过,如果图中的拐角∠A=150°,∠B=120°,三次拐弯后的道路CE与原来公路DA平行,试求出∠C的度数.
如图所示,一条公路修到湖边时,为了保护生态环境,需拐弯绕湖而过,如果图中的拐角∠A=150°,∠B=120°,三次拐弯后的道路CE与原来公路DA平行,试求出∠C的度数.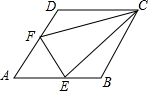 如图,菱形ABCD中,∠A=60°,点E、F分别是边AB、AD上的点,且满足∠BCE=∠DCF,连接EF,当AF=$\sqrt{5}$时,求EF的长.
如图,菱形ABCD中,∠A=60°,点E、F分别是边AB、AD上的点,且满足∠BCE=∠DCF,连接EF,当AF=$\sqrt{5}$时,求EF的长.