Question

2．已知如图：二次函数y=x²-2x-3，根据图象回答下列问题：
（1）设函数图象与x轴交于A、B两点（A在B的左边），与y轴交于点C，求△ABC的面积．
（2）在抛物线的对称轴上找一点P，使PA+PC最小，求出点P的坐标．
（3）若在抛物线和x轴所围成的封闭图形内画出一个最大的正方形，使得正方形的一边在x轴上，其对边的两个端点在抛物线上，试求出这个最大正方形的边长．
（4）翻折x轴下方的图象，在形成的新图象中，当直线y=x+b与新图象有三个交点时，则b的值为1或$\frac{13}{4}$．

Answer 1

分析 （1）令x=0可求得y=-3，故此点C（0，-3），令y=0可求得x₁=3，x₂=-1，从而可求得点A、B的坐标，最后利用三角形的面积公式可求得△ABC的面积；
（2）连接CB交抛物线的对称轴与点P，由轴对称图形的性质可知PA=PB，故此PA+PC=PB+PC，当点B、P、C在同一条直线上时，点PA+PC=BC有最小值，利用待定系数法求得BC的解析式为y=x-3，将x=1代入可求得点P的坐标；
（3）设点C′的坐标为（x，x²-2x-3），由抛物线的对称性可知点D′的横坐标坐标为2-x，从而可求得C′D′=2-2x，由正方形的性质可知2-2x=-（x²-2x-3），x₁=2-$\sqrt{5}$，x₂=2+$\sqrt{5}$（舍去），故此C′D′=$\sqrt{5}$，正方形的面积为5；
（4）如图4所示，直线经过点A时，与新函数图象有3个交点，如图5所示直线与先函数图形有三个交点，从而可求得点b的值．

解答 解：如图1所示：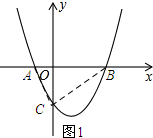

∵令x=0，得y=-3，
∴OC=3．
∵令y=0得：x²-2x-3=0，解得：x₁=3，x₂=-1，
∴A（-1，0）、B（3，0）．
∴AB=4．
∴△ABC的面积=$\frac{1}{2}AB•OC$=$\frac{1}{2}×4×3$=6．
（2）如图2所示：连接BC，交抛物线的对称轴与点P，连接AP．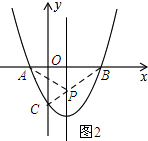

∵x=-$\frac{b}{2a}$，
∴抛物线的对称轴为x=1．
∵点A与点B关于x=1对称，
∴PA=PB．
∴PA+PC=PB+PC．
当点C、P、B在一条直线上时，PA+PC有最小值．
设BC的解析式为y=kx+b，将点B、C的坐标代入得：$\left\{\begin{array}{l}{3k+b=0}\\{b=-3}\end{array}\right.$
解得：k=1，b=-3．
∴直线BC的解析式为y=x-3．
将x=1代入得：y=1-3=-2．
∴P（1，-2）．
（3）如图所示：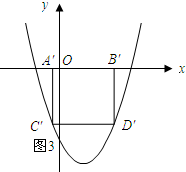

设点C′的坐标为（x，x²-2x-3）．
∵点C′与D′关于x=1对称，
∴点D′的横坐标为2-x．
∴C′D′=2-2x．
∵四边形A′B′D′C′是正方形，
∴A′C′=C′D′．
∴2-2x=-（x²-2x-3）．
解得：x₁=2-$\sqrt{5}$，x₂=2+$\sqrt{5}$（舍去），
∴C′D′=$\sqrt{5}$．
∴正方形的面积为5．
（4）如图4所示，当直线y=x+b经过点A时．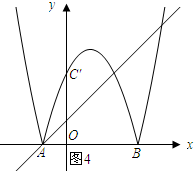

将A（-1，0）代入直线的解析式得：-1+b=0，解得：b=1．
如图5所示：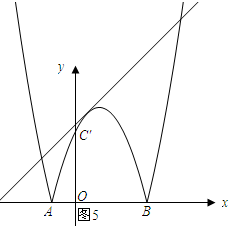

设经过点A、B、C′的抛物线的解析式为y=a（x+1）（x-3），将点C′的坐标代入得：-3a=3，解得a=-1．
∵a=-1，
∴抛物线的解析式为y=-x²+2x+3．
将y=-x²+2x+3与y=x+b联立得：-x²+2x+3=x+b．
∵直线y=x+b与抛物线y=-x²+2x+3有一个公共点，
∴方程x²-x+b-3=0判别式为0．
∴1²-4×1×（b-3）=0．
解得：b=$\frac{13}{4}$．
综上所述，当b=1或b=$\frac{13}{4}$时，直线y=x+b与先函数图象有3个交点．
故答案为：1或$\frac{13}{4}$．

点评 本题主要考查的是二次函数的综合应用，涉及的知识点包括二次函数的图象和性质、函数图象与坐标轴的交点、正方形的性质、轴对称路径最短问题，依据轴对称图形的性质得到当点C、P、B在一条直线上时，PA+PC有最小值是解决问题（2）的关键；依据正方形的四条边相等列出关于x的方程是解答本题（3）的关键；依据一元二次方程根与的判别式求得b的值是解决问题（4）的关键．