题目内容
| 1 | ||||
|
| ||||||||
(
|
| ||||
(
|
| 2 |
| 1 |
| 1 | ||||
|
| ||||||||
(
|
| ||||
(
|
| 3 |
| 2 |
(1)按照上述解题过程的思路,解答
| 1 | ||||
|
(2)利用上述解题结果中的规律计算:
(
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 2008 |
考点:分母有理化
专题:规律型
分析:(1)先分子和分母都乘以
-
,即可求出答案;
(2)根据规律得出原式=(
-
+
-
+
-
+…+
-
)×(
+1),合并后根据平方差公式求出即可.
| 4 |
| 3 |
(2)根据规律得出原式=(
| 2 |
| 1 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2008 |
| 2007 |
| 2008 |
解答:解:(1)
=
=
=
-
=2-
;
(2)(
+
+
+…+
)(
+1)
=(
-
+
-
+
-
+…+
-
)×(
+1)
=(
-1)×(
+1)
=2008-1
=2007.
| 1 | ||||
|
=
| ||||||||
(
|
=
| ||||
| 4-3 |
=
| 4 |
| 3 |
=2-
| 3 |
(2)(
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 2008 |
=(
| 2 |
| 1 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2008 |
| 2007 |
| 2008 |
=(
| 2008 |
| 2008 |
=2008-1
=2007.
点评:本题考查了分母有理化,平方差公式的应用,解此题的关键是能根据求出的算式得出规律.

练习册系列答案
相关题目
 在长方形ABCD中,AD=8cm,AB=6cm,沿对角线BD把△BCD翻折至△BDE,如图.
在长方形ABCD中,AD=8cm,AB=6cm,沿对角线BD把△BCD翻折至△BDE,如图. 如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,求∠A、∠ACD、∠D之间的数量关系.
如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,求∠A、∠ACD、∠D之间的数量关系.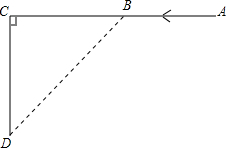 如图,快艇和轮船分别从A地和C地同时开出,航行路线互相垂直.快艇的速度为40千米/时,轮船的速度是15千米/时,A,C两地间的距离是120千米.问经过多少时间,快艇和轮船之间的距离最小?(精确到0.1小时)
如图,快艇和轮船分别从A地和C地同时开出,航行路线互相垂直.快艇的速度为40千米/时,轮船的速度是15千米/时,A,C两地间的距离是120千米.问经过多少时间,快艇和轮船之间的距离最小?(精确到0.1小时)