题目内容
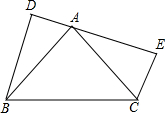
如图，已知D为△ABC边BC延长线上一点，DF⊥AB于F交AC于E，求∠A、∠ACD、∠D之间的数量关系．考点：三角形内角和定理
专题：
分析：先根据DF⊥AB得出∠AFE=90°，故∠A+∠AEF=90°，再根据∠AEF与∠CEF是对顶角可得出∠AEF=∠CEF，再由三角形内角和定理即可得出结论．
解答：解：∵DF⊥AB，
∴∠AFE=90°，
∴∠A+∠AEF=90°，即∠AEF=90°-∠A．
∵∠AEF与∠CEF是对顶角，
∴∠AEF=∠CEF，
∵∠ACD+∠D+∠CEF=180°，
∴∠ACD+∠D+90°-∠A=180°，即∠ACD+∠D-∠A=90°．
∴∠AFE=90°，
∴∠A+∠AEF=90°，即∠AEF=90°-∠A．
∵∠AEF与∠CEF是对顶角，
∴∠AEF=∠CEF，
∵∠ACD+∠D+∠CEF=180°，
∴∠ACD+∠D+90°-∠A=180°，即∠ACD+∠D-∠A=90°．
点评：本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．
练习册系列答案
相关题目
如图，在△ABC中，AB=AC，BD、CE垂直于过点A的直线，垂足分别为D、E，若AD=CE，问∠BAC=