题目内容

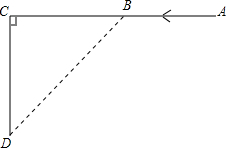如图，快艇和轮船分别从A地和C地同时开出，航行路线互相垂直．快艇的速度为40千米/时，轮船的速度是15千米/时，A，C两地间的距离是120千米．问经过多少时间，快艇和轮船之间的距离最小？（精确到0.1小时）
考点：勾股定理的应用
专题：
分析：直接利用勾股定理以及二次函数最值求法得出即可．
解答：解：设经x小时，快艇和轮船之间的距离最小，由题意得：
BD=
BC2+DC2
=
(120-40x)2+(15x)2
=5
10(x-0.3)2+575.1
，（0≤x≤3），
当x=0.3时，BD最小．
答：经过0.3小时，快艇和轮船之间的距离最小．
点评：此题主要考查了勾股定理的应用以及二次函数最值求法，正确配方得出是解题关键．
练习册系列答案
相关题目
行驶中的汽车，在刹车后由于惯性的作用，还要继续向前滑行一段距离才停止，这段距离称为“刹车距离”，为了测定某种型号汽车的刹车性能（车速不超过130km/h），对这种汽车进行测试，测得数据如下表：
刹车时车速/（km/h）0102030405060
刹车距离/m01.12.43.95.67.59.6
（1）以车速为x轴，以刹车距离为y轴，在坐标系中描出这些数据所表示的点，并用平滑的曲线连接这些点，得到函数的大致图象；
（2）观察图象，估计函数的类型，并确定一个满足这些数据的函数解析式；
（3）该型号汽车在国道上发生了一次交通事故，现场测得刹车距离为26.4m，请推测刹车时的速度是多少？请问在事故发生时，汽车是超速行驶还是正常行驶？
1
2
+
1
=
2
-
1
(
2
+
1
)(
2
-
1
)
=
2
-
1
(
2
)2-(
1
)2
=
2
-
1

1
3
+
2
=
3
-
2
(
3
+
2
)(
3
-
2
)
=
3
-
2
(
3
)2-(
2
)2
=
3
-
2

（1）按照上述解题过程的思路，解答
1
4
+
3
；
（2）利用上述解题结果中的规律计算：
（
1
2
+
1
+
1
3
+
2
+
1
4
+
3
+…+
1
2008
+
2007
）（
2008
+1）
计算：12÷（-3-
1
4
+
4
3
）．
已知
b
a
+
a
b
=3，求[1+2b2（a2-b2）-1]÷[1+2b（a-b）-1]．
你在心里想好一个两位数，将十位数字乘二，然后加三，再将所得的新数乘五，最后将得到的数加个位数字，把你的结果告诉我，我就知道你心里想的两位数．你知道小明是怎样算出来的么？请解释其中的道理．
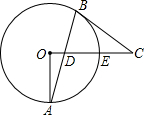如图，⊙O中，半径OA⊥OE，过B作⊙O的切线，交OE的延长线与C，OA=3，BC=4，求AD的长．
解方程：（10-x）（500-10x）=8000．
任写一个5次单项式，满足（1）只含字母x，y；（2）系数为-1
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网