题目内容
15.下列多项式中,不能用公式法分解因式的是( )| A. | (x+y)2+12(x+y)+36 | B. | -x2+2xy-y2 | C. | -4x2+9y2 | D. | x2+y2 |
分析 各项利用平方差公式及完全平方公式判断即可得到结果.
解答 解:A、原式=(x+y+6)2,不合题意;
B、原式=-(x-y)2,不合题意;
C、原式=(3y+2x)(3y-2x),不合题意;
D、原式不能分解,符合题意,
故选D
点评 此题考查了因式分解-运用公式法,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
3.计算$\sqrt{12}$-$\sqrt{\frac{3}{4}}$的结果正确的是( )
| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{8}$ | D. | 0 |
7.某公司招聘人才,对应聘者分别进行阅读能力、专业知识、表达能力三项测试,并将三项测试得分按3:5:2的比例确定每人的最终成绩,现欲从甲乙两选手中录取一人,已知两人的各项测试得分如下表(单位:分)
①请通过相关的计算说明谁将被录用?
②请对落选者今后的应聘提些合理的建议.
| 阅读 | 专业 | 表达 | |
| 甲 | 93 | 86 | 73 |
| 乙 | 95 | 81 | 79 |
②请对落选者今后的应聘提些合理的建议.
4.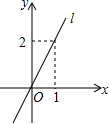 如图,把直线L沿y轴向下平移2个单位得到直线L′,则直线L′的解析式为( )
如图,把直线L沿y轴向下平移2个单位得到直线L′,则直线L′的解析式为( )
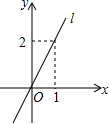 如图,把直线L沿y轴向下平移2个单位得到直线L′,则直线L′的解析式为( )
如图,把直线L沿y轴向下平移2个单位得到直线L′,则直线L′的解析式为( )| A. | y=2x+1 | B. | y=2x-4 | C. | y=2x-2 | D. | y=-2x+2 |
5.利用配方法将x2-2x+3=0化为a(x-h)2+k=0 (a≠0)的形式为 ( )
| A. | (x-1)2-2=0 | B. | (x-1)2+2=0 | C. | (x+1)2+2=0 | D. | (x+1)2-2=0 |
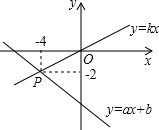 如图,已知函数y=ax+b和y=kx的图象交于点P,根据图象可直接得关于x的不等式ax+b≥kx的解集是x≤-4.
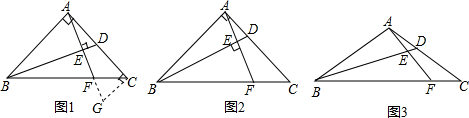
如图,已知函数y=ax+b和y=kx的图象交于点P,根据图象可直接得关于x的不等式ax+b≥kx的解集是x≤-4.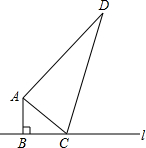 如图,∠ABC=90°,AB=6cm,AD=24cm,BC+CD=34cm,C是直线l上一动点,请你探索当C离B多远时,△ACD是一个以CD为斜边的直角三角形?
如图,∠ABC=90°,AB=6cm,AD=24cm,BC+CD=34cm,C是直线l上一动点,请你探索当C离B多远时,△ACD是一个以CD为斜边的直角三角形?