题目内容
3.先化简,再求值:$\frac{x-1}{x}÷\frac{{x}^{2}-1}{{x}^{2}+2x}-1$,其中x=|2-$\sqrt{3}$|+2sin60°.分析 首先把分式的除法转化为乘法,然后通分相减即可化简,再化简x的值,代入求值即可.
解答 解:原式=$\frac{x-1}{x}$•$\frac{x(x+2)}{(x+1)(x-1)}$-1
=$\frac{x+2}{x+1}$-1
=$\frac{x+2-(x+1)}{x+1}$
=$\frac{1}{x+1}$,
当x=|2-$\sqrt{3}$|+2sin60°=2-$\sqrt{3}$+2×$\frac{\sqrt{3}}{2}$=2时,原式=$\frac{1}{3}$.
点评 本题考查了分式的化简求值,正确对分式进行通分、约分变形,正确进行分解因式是关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
13.若把分式$\frac{x+3y}{2x}$的x、y同时扩大为原来的2倍,则分式的值( )
| A. | 扩大2倍 | B. | 缩小2倍 | C. | 不变 | D. | 缩小3倍 |
12.将一质地均匀的正方体骰子掷一次,观察向上一面的点数,与点数3的差不大于2的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
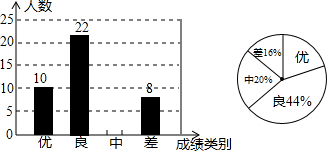
18.学校开展“阳光体育活动”,对六年级同学参加体育锻炼的情况作了调查,结果如表.
(1)女生中,天天锻炼的占女生总数的百分之几?不锻炼的呢?
(2)男生中,每种情况的男生各占百分之几?然后根据计算结果绘制男生参加体育锻炼情况的扇形统计图.
| 锻炼情况 | 女生 | 男生 |
| 天天锻炼 | 20 | 27 |
| 不经常锻炼 | 18 | 24 |
| 不锻炼 | 12 | 9 |
(2)男生中,每种情况的男生各占百分之几?然后根据计算结果绘制男生参加体育锻炼情况的扇形统计图.
 在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公共点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是b>2或b<-2.
在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公共点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是b>2或b<-2.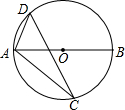 如图,AB是⊙O的直径,△ACD内接于⊙O,若∠BAC=42°,则∠ADC=48°.
如图,AB是⊙O的直径,△ACD内接于⊙O,若∠BAC=42°,则∠ADC=48°.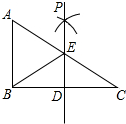 如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于$\frac{1}{2}$BC长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=$\frac{1}{2}$AB中,正确的个数为( )
如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于$\frac{1}{2}$BC长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=$\frac{1}{2}$AB中,正确的个数为( )