题目内容
如图①,已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.

(1)求证:EG=CG;
(2)如图②所示,当点F与BC的延长线相交时,判断EG与CG的关系,并加以证明.

(1)求证:EG=CG;
(2)如图②所示,当点F与BC的延长线相交时,判断EG与CG的关系,并加以证明.
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)根据直角三角形斜边上的中线等于斜边的一半,EG=
DF,CG=
DF,所以EG=CG.
(2)当点F与BC的延长线相交时,EG=CG,根据(1)的证明思路即可证明成立.
| 1 |
| 2 |
| 1 |
| 2 |
(2)当点F与BC的延长线相交时,EG=CG,根据(1)的证明思路即可证明成立.
解答:(1)证明:∵EF⊥BD,
∴△DEF为直角三角形,
∵G为DF中点,
∴EG=
DF,(直角三角形斜边上的中线等于斜边的一半),
在正方形ABCD中,∠BCD=90°,
又G为DF中点,
∴CG=
DF,(直角三角形斜边上的中线等于斜边的一半),
∴EG=CG;
(2)当点F与BC的延长线相交时,EG=CG,
理由如下:∵EF⊥BD,
∴△DEF为直角三角形,
∵G为DF中点,
∴EG=
DF,
在正方形ABCD中,∠BCD=90°,
∴∠DCF=90°,
又∵G为DF中点,
∴CG=
DF,
∴EG=CG.
∴△DEF为直角三角形,
∵G为DF中点,
∴EG=
| 1 |
| 2 |
在正方形ABCD中,∠BCD=90°,
又G为DF中点,
∴CG=
| 1 |
| 2 |
∴EG=CG;
(2)当点F与BC的延长线相交时,EG=CG,
理由如下:∵EF⊥BD,
∴△DEF为直角三角形,
∵G为DF中点,
∴EG=
| 1 |
| 2 |
在正方形ABCD中,∠BCD=90°,
∴∠DCF=90°,
又∵G为DF中点,
∴CG=
| 1 |
| 2 |
∴EG=CG.
点评:本题主要考查了正方形的性质以及直角三角形斜边上的中线等于斜边的一半的性质,熟练掌握性质是解题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、三角形的角平分线是射线 |
| B、过三角形的顶点,且过对边中点的直线是三角形的一条中线 |
| C、一个三角形同一边上的中线、高及这条边所对的角的平分线中,高最短 |
| D、三角形的高、中线、角平分线一定在三角形的内部 |
 解不等式组:
解不等式组: 如图,△ABC为等边三角形,D为BC边上一点,以AD为边作∠ADE=60°,DE与△ABC的外角平分线CE交于点E.
如图,△ABC为等边三角形,D为BC边上一点,以AD为边作∠ADE=60°,DE与△ABC的外角平分线CE交于点E.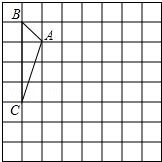 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求解决下列问题:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求解决下列问题: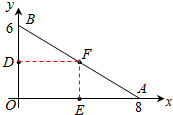 已知抛物线y=ax2+bx+c(a≠0).若抛物线经过点A,则记为yA;若经过点A、B,则记为yAB;若经过点A、B、C,则记为yABC.
已知抛物线y=ax2+bx+c(a≠0).若抛物线经过点A,则记为yA;若经过点A、B,则记为yAB;若经过点A、B、C,则记为yABC.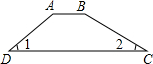 随着“碰瓷”事件的频繁发生,现在老人摔倒了敢不敢扶成了一个热门话题,前段时间郑州市的一群老人针对这个现象进行了一场名为“请放心扶起我”的行为艺术,为了扩大行为艺术的影响,纠正社会风气,某老年艺术团准备举行一场义演,请你为义演舞台的选址出谋划策,如图:舞台宽度为5米,左面楼梯长3米,梯面与地面夹角∠1为40°,右面有个专供残疾演员登台用的斜坡,与地面夹角∠2为30°,且台面AB与地面DC平行,请你通过计算说明至少空地面有多宽才能搭建下这个舞台(结果保留两位小数)?(
随着“碰瓷”事件的频繁发生,现在老人摔倒了敢不敢扶成了一个热门话题,前段时间郑州市的一群老人针对这个现象进行了一场名为“请放心扶起我”的行为艺术,为了扩大行为艺术的影响,纠正社会风气,某老年艺术团准备举行一场义演,请你为义演舞台的选址出谋划策,如图:舞台宽度为5米,左面楼梯长3米,梯面与地面夹角∠1为40°,右面有个专供残疾演员登台用的斜坡,与地面夹角∠2为30°,且台面AB与地面DC平行,请你通过计算说明至少空地面有多宽才能搭建下这个舞台(结果保留两位小数)?(