题目内容
17.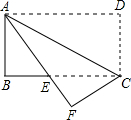 如图,在长方形纸片ABCD中,AB=8,AD=16,将它沿着对角线AC对折,使点D落在点F处,AF交BC于点E.
如图,在长方形纸片ABCD中,AB=8,AD=16,将它沿着对角线AC对折,使点D落在点F处,AF交BC于点E.(1)试说明:AE=EC;
(2)求BE的长.
分析 (1)根据矩形的性质得到AD∥BC,由平行线的性质得到∠DAC=∠ACB,由△AFC是由△ADC沿着AC折叠得到的,得到∠FAC=∠DAC,等量代换得到∠FAC=∠ACE,根据等腰三角形的性质得到结论;
(2)根据AE=CE,再利用勾股定理求得AE的长.
解答 解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵△AFC是由△ADC沿着AC折叠得到的,
∴∠FAC=∠DAC,
∴∠FAC=∠ACE,
∴AE=CE;
(2)∵BC=AD=8,∠B=90°,
∴AE2=AB2+BE2,
即:(8-BE)2=42+BE2,
∴BE=3.
点评 此题考查了翻折变换-折叠问题,矩形的性质,勾股定理,平行线的性质,等腰三角形的判定,熟练正确折叠的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
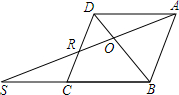 菱形ABCD中,O对角线BD上一点,连接AO并延长,与DC交于点R,与BC的延长线交于点S,若AD=4,∠DCB=60°,BS=10,求CR、OD和AR的长.
菱形ABCD中,O对角线BD上一点,连接AO并延长,与DC交于点R,与BC的延长线交于点S,若AD=4,∠DCB=60°,BS=10,求CR、OD和AR的长.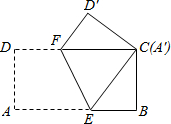 如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则DF的长为3.
如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则DF的长为3.