题目内容
19.某校初一年级学生进行秋季拔河比赛,甲、乙两班进入最后的决赛.比赛规定:当绳子中间的红的标志物距离初始位置超过2米时.红色标志物所在区域的班级获胜.随着裁判员的一声哨响,比赛开始,红色标志物先向乙队方向移动了0.2米,又向甲队方向移动了0.5米;相持了一会后,又向乙队方向移动0.4米,随后又向甲队方向移动了1.3米,在大家的欢呼中,最后标志物又向甲队方向移动了0.9米.此时可以决出胜负吗?哪个班级获胜?请说明理由.分析 首先设定向甲班移动为正,向乙班移动为负,然后根据题目中的数据进行相加,看最后的结果,然后与s进行比较,即可解答本题.
解答 解:此时可以决出胜负,甲班获胜.
理由:设向甲班移动为正,向乙班移动为负,
则(-0.2)+0.5+(-0.4)+1.3+0.9=2.1>2,
故甲班获胜,
即此时可以决出胜负,甲班获胜.
点评 本题考查数轴,解题的关键是规定正方向,灵活变化,能说明问题是否成立的理由.

练习册系列答案
相关题目
10.下列说法错误的是( )
| A. | -1的立方根是-1 | B. | 1的平方根是1 | C. | $\sqrt{2}$是2的平方根 | D. | -3是9的平方根 |
14.下列各式不是方程的是( )
| A. | 3x2+4=5 | B. | m+2n=0 | C. | x=-3 | D. | 4y>3 |
4.若7x3y3与一个多项式的积是28x7y3-21x5y5+2y•(7x3y3)2,则这个多项式为( )
| A. | 4x4-3x2y2+14x3y4 | B. | 4x2y-3x2y2 | ||
| C. | 4x4-3y2 | D. | 4x4-3xy2+7xy3 |
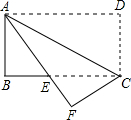 如图,在长方形纸片ABCD中,AB=8,AD=16,将它沿着对角线AC对折,使点D落在点F处,AF交BC于点E.
如图,在长方形纸片ABCD中,AB=8,AD=16,将它沿着对角线AC对折,使点D落在点F处,AF交BC于点E.