题目内容
2.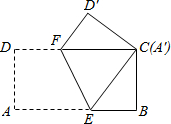 如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则DF的长为3.
如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则DF的长为3.
分析 根据翻折变换的性质可得∠1=∠2,AE=CE,用CE表示出BE,然后在Rt△BCE中,利用勾股定理列出方程求出CE,再根据两直线平行,内错角相等可得∠1=∠3,求出∠2=∠3,根据等角对等边可得FC=CE,从而得解.
解答 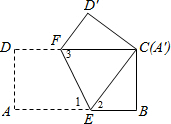 解:如图,∵矩形纸片ABCD折叠后点A与C重合,
解:如图,∵矩形纸片ABCD折叠后点A与C重合,
∴∠1=∠2,AE=CE,
∴BE=AB-AE=8-CE,
在Rt△BCE中,BE2+BC2=CE2,
即(8-CE)2+42=CE2,
解得CE=5,
∵矩形ABCD的边AB∥CD,
∴∠1=∠3,
∴∠2=∠3,
∴FC=CE=5,
∴DF=8-5=3.
故答案为:3.
点评 本题考查了翻折变换的性质,勾股定理的应用,熟记翻折前后的两个图形能够重合得到相等的边和角是解题的关键.

练习册系列答案
相关题目
4.若7x3y3与一个多项式的积是28x7y3-21x5y5+2y•(7x3y3)2,则这个多项式为( )
| A. | 4x4-3x2y2+14x3y4 | B. | 4x2y-3x2y2 | ||
| C. | 4x4-3y2 | D. | 4x4-3xy2+7xy3 |
14.下列各组数中,相等的是( )
| A. | -1与(-4)+(-3) | B. | 3与-(-3) | C. | $\frac{3^2}{4}$与$\frac{9}{16}$ | D. | |-16|与-16 |
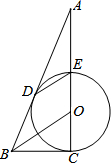 如图,CE是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线,交CE延长线于点A,连接DE,过点O作OB∥ED,交AD的延长线于点B,连接BC.
如图,CE是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线,交CE延长线于点A,连接DE,过点O作OB∥ED,交AD的延长线于点B,连接BC.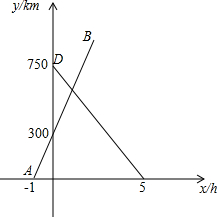 铁路中心记录途经南京的各型号列车行驶情况,如图,上午7:00为起始时间,列车x小时后距南京y千米,线段AB和DE分别表示一辆动车和一辆特快列车行驶过程中y与x的函数关系,点A坐标为(-1,0),点B坐标为(2,900).
铁路中心记录途经南京的各型号列车行驶情况,如图,上午7:00为起始时间,列车x小时后距南京y千米,线段AB和DE分别表示一辆动车和一辆特快列车行驶过程中y与x的函数关系,点A坐标为(-1,0),点B坐标为(2,900).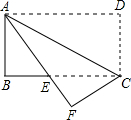 如图,在长方形纸片ABCD中,AB=8,AD=16,将它沿着对角线AC对折,使点D落在点F处,AF交BC于点E.
如图,在长方形纸片ABCD中,AB=8,AD=16,将它沿着对角线AC对折,使点D落在点F处,AF交BC于点E.