题目内容
5.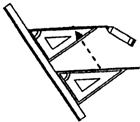 如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )
如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )| A. | 两直线平行,同位角相等 | B. | 两直线平行,内错角相等 | ||
| C. | 同位角相等,两直线平行 | D. | 内错角相等,两直线平行 |
分析 根据∠BAC=∠EDC,由同位角相等,两直线平行,即可判定AB∥DE.
解答 解:∵∠BAC=∠EDC,
∴AB∥DE.
故选C.
点评 本题考查的是平行线的判定定理,即同位角相等,两直线平行.

练习册系列答案
相关题目
16. 如图,?ABCD中,AB=13,AD=10,将?ABCD沿AE翻折后,点B恰好与点C重合,则点C到AD的距离为( )
如图,?ABCD中,AB=13,AD=10,将?ABCD沿AE翻折后,点B恰好与点C重合,则点C到AD的距离为( )
 如图,?ABCD中,AB=13,AD=10,将?ABCD沿AE翻折后,点B恰好与点C重合,则点C到AD的距离为( )
如图,?ABCD中,AB=13,AD=10,将?ABCD沿AE翻折后,点B恰好与点C重合,则点C到AD的距离为( )| A. | 5 | B. | 12 | C. | 3 | D. | $\sqrt{69}$ |
13.已知实数x、y满足(x-3)2+$\sqrt{y-7}$=0,则以x、y的值为两边长的等腰三角形的周长是( )
| A. | 13或17 | B. | 13 | C. | 17 | D. | 无法确定 |
20.下列命题正确的是( )
| A. | 若m>n则mc>nc | B. | 若m+c2>n+c2,则m>n | ||
| C. | 若m>b,b<c,则m>c | D. | 若m>n,则mc2>nc2 |
10.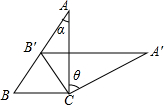 如图,△ABC中,∠ACB=90°,∠A=α,以点C为中心将△ABC顺时针旋转θ角,得到△A′B′C′,且B′点恰好落在AB上,则旋转角θ的大小为( )
如图,△ABC中,∠ACB=90°,∠A=α,以点C为中心将△ABC顺时针旋转θ角,得到△A′B′C′,且B′点恰好落在AB上,则旋转角θ的大小为( )
 如图,△ABC中,∠ACB=90°,∠A=α,以点C为中心将△ABC顺时针旋转θ角,得到△A′B′C′,且B′点恰好落在AB上,则旋转角θ的大小为( )
如图,△ABC中,∠ACB=90°,∠A=α,以点C为中心将△ABC顺时针旋转θ角,得到△A′B′C′,且B′点恰好落在AB上,则旋转角θ的大小为( )| A. | α+10° | B. | α+20° | C. | α | D. | 2α |
17.下列运算正确的是( )
| A. | x2÷x-3=x5 | B. | (a+2b)2=a2+2ab+4b2 | ||
| C. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | D. | (x2y3)2=x4y9 |
14.根据函数y=$\frac{1}{x}$的图象,判断当x≥-1时,y的取值范围是( )
| A. | y<-1 | B. | y≤-1 | C. | y≤-1或y>0 | D. | y<-1或y≥0 |
15.从分别标有数-3,-2,-1,0,1,2,3的七张没有明显差别的卡片中,随机抽取一张,所抽卡片上的数的绝对值不是正数的概率是( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
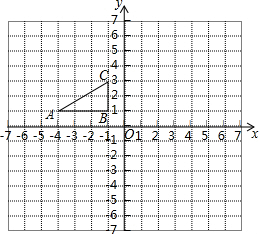 如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上.建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-1,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上.建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-1,1).