题目内容
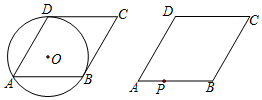
16. 如图,?ABCD中,AB=13,AD=10,将?ABCD沿AE翻折后,点B恰好与点C重合,则点C到AD的距离为( )
如图,?ABCD中,AB=13,AD=10,将?ABCD沿AE翻折后,点B恰好与点C重合,则点C到AD的距离为( )| A. | 5 | B. | 12 | C. | 3 | D. | $\sqrt{69}$ |
分析 由点B恰好与点C重合,可知AE垂直平分BC,根据勾股定理计算AE的长即可.
解答 解:∵翻折后点B恰好与点C重合,
∴AE⊥BC,BE=CE,
∵BC=AD=10,
∴BE=5,
∴AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=12,
∵AD∥BC,
∴点C到AD的距离=AE,
故点C到AD的距离是12,
故选B.
点评 本题考查了翻折变换,平行四边形的性质,勾股定理,根据翻折特点发现AE垂直平分BC是解决问题的关键.

练习册系列答案
相关题目
11.今年某县有1万名初中和小学生参加全国义务教育质量抽测,为了了解1万名学生的抽测成绩,从中抽取500名学生抽测成绩进行统计分析,在这个问题中数据500是( )
| A. | 总体 | B. | 个体 | C. | 一个样本 | D. | 样本容量 |
1.一次函数y=(2a-1)x+6的图象与坐标轴在第二象限围成的三角形的面积为6,则a的值为( )
| A. | a=2 | B. | a=-2 | C. | a=1 | D. | a=-1 |
8.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.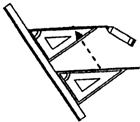 如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )
如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )
 如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )
如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )| A. | 两直线平行,同位角相等 | B. | 两直线平行,内错角相等 | ||
| C. | 同位角相等,两直线平行 | D. | 内错角相等,两直线平行 |
6.若二次根式$\sqrt{2x-6}$在实数范围内有意义,则x的取值范围是( )
| A. | x≤3 | B. | x>3 | C. | x≥3 | D. | x>-3 |