题目内容
10.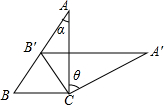 如图,△ABC中,∠ACB=90°,∠A=α,以点C为中心将△ABC顺时针旋转θ角,得到△A′B′C′,且B′点恰好落在AB上,则旋转角θ的大小为( )
如图,△ABC中,∠ACB=90°,∠A=α,以点C为中心将△ABC顺时针旋转θ角,得到△A′B′C′,且B′点恰好落在AB上,则旋转角θ的大小为( )| A. | α+10° | B. | α+20° | C. | α | D. | 2α |
分析 由旋转的性质可知BC=B′C,∠ACA'=∠BCB'=θ,进而得到∠CBB'=90°-α=∠CB'B,在等腰△CBB'中,根据三角形内角和定理可得2(90°-α)+θ=180°,由此可得旋转角θ的大小.
解答 解:由旋转得BC=B′C,∠ACA'=∠BCB'=θ,
而∠A=α,∠ABC=90°-α,
∴等腰△CBB'中,∠CBB'=90°-α=∠CB'B,∠BCB'=θ,
∵△CBB'中,∠CBB'+∠B+∠BCB'=180°,
∴2(90°-α)+θ=180°,
∴θ=2α,
故选:D.
点评 本题主要考查了旋转的性质,等腰三角形的性质以及三角形内角和定理的综合应用,解题时注意:对应点与旋转中心所连线段的夹角等于旋转角,旋转前、后的图形全等.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
20.下列交通标志中,可以看作是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.一次函数y=(2a-1)x+6的图象与坐标轴在第二象限围成的三角形的面积为6,则a的值为( )
| A. | a=2 | B. | a=-2 | C. | a=1 | D. | a=-1 |
5.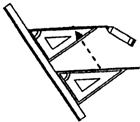 如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )
如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )
 如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )
如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )| A. | 两直线平行,同位角相等 | B. | 两直线平行,内错角相等 | ||
| C. | 同位角相等,两直线平行 | D. | 内错角相等,两直线平行 |
15.-52的倒数是( )
| A. | 25 | B. | -25 | C. | $\frac{1}{25}$ | D. | -$\frac{1}{25}$ |
2.|-2017|的相反数是( )
| A. | 2017 | B. | $\frac{1}{2017}$ | C. | -2017 | D. | -$\frac{1}{2017}$ |
19.分解因式:x2y-4y结果正确的是( )
| A. | y(x2-4) | B. | y(x-2)2 | C. | y(x+2)2 | D. | y(x+2)(x-2) |
20. 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )
 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=4$\sqrt{3}$,则圆锥底面圆的半径是( )| A. | $\frac{4}{3}$ | B. | $\frac{2}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
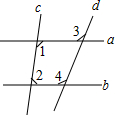 如图,若∠1+∠2=180°,∠3=110°,则∠4=110°.
如图,若∠1+∠2=180°,∠3=110°,则∠4=110°.