题目内容
6．
如图所示，AD∥BC，AB∥DC，M，Q分别在DA、BC的最长线上，且AM=CQ，连接MQ，分别交CD，BD，AB于点P，E，N，求证：△AMN≌△CQP．
分析 根据平行线的性质得出∠QCP=∠MAN，∠Q=∠M，根据ASA证△AMN≌△CQP即可．
解答 证明：∵AD∥BC，AB∥DC
∴∠QCP=∠MAN，∠Q=∠M，
∵在△AMN和△CQP中
$\left\{\begin{array}{l}{∠QCP=∠MAN}\\{AM=CQ}\\{∠Q=∠M}\end{array}\right.$，
∴△AMN≌△CQP（ASA），
点评 此题主要考查了平行线的性质，全等三角形的判定，熟练掌握三角形全等的判定方法是解此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
△ABC中，∠A=30°，∠B=45°，AC=4，求AB的长？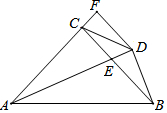
如图，在△ABC中，AC=BC，∠ACB=90°，AE平分∠BAC交BC于E，BD⊥AE于 D，DF⊥AC交AC的延长线于F，连接CD，给出四个结论：
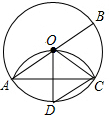已知：如图，AB是⊙O的直径，AC是弦，将劣弧$\widehat{AC}$沿弦AC翻折与AB的交点恰好是圆心O，连接BC，作半径OD⊥AC．求证：四边形BCDO是菱形．
如图，△ABC是等边三角形，D是BC上一点，∠ADE=60°，∠BCE=120°，CE、DE交于E；