题目内容
1．已知等腰三角形的两腰是关于x的一元二次方程x2-kx+4=0的两根，则k=4．分析 由等腰三角形的性质可值方程x2-kx+4=0有两个相等的实数根，根据根的判别式即可得出关于k的一元二次方程，解方程可得出k的值，经验证后k=-4不合适，此题的解．
解答 解：∵等腰三角形的两腰是关于x的一元二次方程x2-kx+4=0的两根，
∴方程x2-kx+4=0有两个相等的实数根，
∴△=（-k）2-4×1×4=k2-16=0，
解得：k=±4，
当k=-4时，原方程为x2+4x+4=（x+2）2=0，
解得：x=-2，
∴k=-4舍去．
故答案为：4．
点评 本题考查了根的判别式以及等腰三角形的性质，根据等腰三角形的性质结合根的判别式得出关于k的一元二次方程是解题的关键．
练习册系列答案
相关题目
如图，在平面直角坐标系中，点P的坐标为（0，8），直线y=$\frac{3}{4}$x-6与x轴、y轴分别交于点A、B，点M是直线AB上的一个动点，则PM长的最小值为$\frac{56}{5}$．
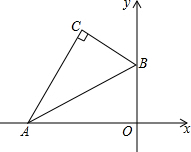如图，在平面直角坐标系中，含30°锐角的三角板的直角顶点C落在第二象限，其斜边两端点A、B分别落在x轴、y轴上，且AB=12cm，OB=6cm．点C′是第二象限内不与点C重合的一个点，且以A、B、C′为顶点的三角形与△ABC相似（相似比不为1），则点C′的坐标为（-6$\sqrt{3}$，24）、（-2$\sqrt{3}$，12）、（-12$\sqrt{3}$，18）和（-8$\sqrt{3}$，6）．
如图：在△ABC中，DE∥FG∥BC，且DE、FG将△ABC的面积三等分，若AB=BC=12cm，求FG和DF的长．
如图所示，AD∥BC，AB∥DC，M，Q分别在DA、BC的最长线上，且AM=CQ，连接MQ，分别交CD，BD，AB于点P，E，N，求证：△AMN≌△CQP．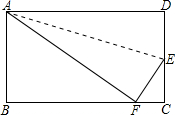
长方形纸片ABCD，沿AE折叠边AD，使点D落在BC边上的点F处，AB=5，S△ABF=30，求EC．
如图，AB与CD交于点O，OA=OC，OD=OB，∠A=50°，∠B=30°，则∠D的度数为30°．