题目内容
12.计算:(1)(-x)•x2•(-x)6
(2)(-2x2)3+x2•x4-(-3x3)2
(3)[-2(x-y)2]2•(y-x)3
(4)${(-\frac{1}{2})^{-2}}+|{-3}|+{(2-\sqrt{3})^0}+{(-1)^{2013}}$.
分析 (1)根据同底数幂的乘法法则计算即可求解;
(2)先算积的乘方、同底数幂的乘法,再合并同类项即可求解;
(3)先算积的乘方、再算同底数幂的乘法即可求解;
(4)先算负整数指数幂、绝对值、零指数幂和乘方,再算加减法即可求解.
解答 解:(1)(-x)•x2•(-x)6
=-x1+2+6
=-x9;
(2)(-2x2)3+x2•x4-(-3x3)2
=-8x6+x6-9x6
=-16x6;
(3)[-2(x-y)2]2•(y-x)3
=4(x-y)4•[-(x-y)3]
=-4(x-y)4+3
=-4(x-y)7;
(4)${(-\frac{1}{2})^{-2}}+|{-3}|+{(2-\sqrt{3})^0}+{(-1)^{2013}}$
=4+3+1-1
=7.
点评 本题主要考查整式的混合运算,同底数幂的乘法,积的乘方,合并同类项,负整数指数幂、绝对值、零指数幂和乘方的运用,熟记公式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.将$\frac{a^2+5ab}{3a-2b}$中的a、b都扩大为原来的4倍,则分式的值( )
| A. | 不变 | B. | 扩大原来的4倍 | C. | 扩大原来的8倍 | D. | 扩大原来的16倍 |
1.已知平行四边形ABCD的周长为32,AB=12,则BC的长为( )
| A. | 4 | B. | 12 | C. | 24 | D. | 28 |
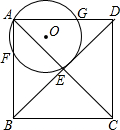 如图,在正方形ABCD中,E为对角线AC,BD的交点,经过点A和点E作⊙O,分别交AB、AD于点F、G.已知正方形边长为5,⊙O的半径为2,则AG•GD的值为9.
如图,在正方形ABCD中,E为对角线AC,BD的交点,经过点A和点E作⊙O,分别交AB、AD于点F、G.已知正方形边长为5,⊙O的半径为2,则AG•GD的值为9.