题目内容
16.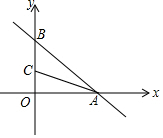 在平面直角坐标系中,已知一次函数y=-$\frac{3}{4}$x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
在平面直角坐标系中,已知一次函数y=-$\frac{3}{4}$x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )| A. | (0,3) | B. | (0,$\frac{4}{3}$) | C. | (0,$\frac{8}{3}$) | D. | (0,$\frac{7}{3}$) |
分析 过C作CD⊥AB于D,先求出A,B的坐标,分别为A(8,0),B(0,6),得到AB的长,再根据折叠的性质得到AC平分∠OAB,得到CD=CO=n,DA=OA=8,则DB=10-8=2,BC=6-n,在Rt△BCD中,利用勾股定理得到n的方程,解方程求出n即可.
解答 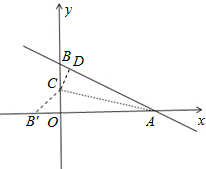 解:过C作CD⊥AB于D,如图,
解:过C作CD⊥AB于D,如图,
对于直线y=-$\frac{3}{4}$x+6,
当x=0,得y=6;当y=0,x=8,
∴A(8,0),B(0,6),即OA=8,OB=6,
∴AB=10,
又∵坐标平面沿直线AC折叠,使点B刚好落在x轴上,
∴AC平分∠OAB,
∴CD=CO=n,则BC=6-n,
∴DA=OA=8,
∴DB=10-8=2,
在Rt△BCD中,DC2+BD2=BC2,
∴n2+22=(6-n)2,解得n=$\frac{8}{3}$,
∴点C的坐标为(0,$\frac{8}{3}$).
故选:C.
点评 本题考查了求直线与坐标轴交点的坐标的方法:分别令x=0或y=0,求对应的y或x的值;也考查了折叠的性质和勾股定理.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
6.对于实数a,b,先定义一种新运算“★”如下:当a≥b时,a★b=a2+ab;当a<b时,a★b=b2+ab;若2★m=24,则实数m等于( )
| A. | 10 | B. | 4 | C. | 4或-6 | D. | 4或-6或10 |
11.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{10}$ | C. | $\sqrt{20}$ | D. | $\sqrt{\frac{1}{3}}$ |
5.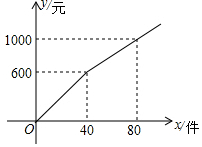 某商店销售一种商品,售出部分商品后进行了降价促销,销售金额y(元)与销售量(x)的函数关系如图所示,则降价后每件商品的销售价格为( )
某商店销售一种商品,售出部分商品后进行了降价促销,销售金额y(元)与销售量(x)的函数关系如图所示,则降价后每件商品的销售价格为( )
 某商店销售一种商品,售出部分商品后进行了降价促销,销售金额y(元)与销售量(x)的函数关系如图所示,则降价后每件商品的销售价格为( )
某商店销售一种商品,售出部分商品后进行了降价促销,销售金额y(元)与销售量(x)的函数关系如图所示,则降价后每件商品的销售价格为( )| A. | 5元 | B. | 10元 | C. | 12.5元 | D. | 15元 |
6.下列命题中,为真命题的是( )
| A. | 如果-2x>-2,那么x>1 | B. | 如果a2=b2,那么a3=b3 | ||
| C. | 面积相等的三角形全等 | D. | 如果a∥b,b∥c,那么a∥c |
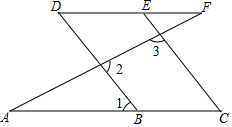 完成推理填空:
完成推理填空: