题目内容
6.对于实数a,b,先定义一种新运算“★”如下:当a≥b时,a★b=a2+ab;当a<b时,a★b=b2+ab;若2★m=24,则实数m等于( )| A. | 10 | B. | 4 | C. | 4或-6 | D. | 4或-6或10 |
分析 根据题意,(1)m≤2时,22+2m=24;(2)m>2时,m2+2m=24;据此求出m的值是多少即可.
解答 解:∵当a≥b时,a★b=a2+ab;当a<b时,a★b=b2+ab,
∴(1)m≤2时,22+2m=24,
解得m=10,不满足题意.
∴(2)m>2时,m2+2m=24,
解得m=-6或4,
∵-6<2,
∴m=4.
综上,可得:m=4.
故选:B.
点评 此题主要考查了实数的运算,以及定义新运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
16.某班期末考试数学的平均成绩为115分方差为768,如果每名学生都多考5分,下列说法正确的是( )
| A. | 平均分不变,方差不变 | B. | 平均分变大,方差不变 | ||
| C. | 平均分不变,方差变大 | D. | 平均分变大,方差变大 |
17.今年我市有1万名考生参加中考,为了了解这些考生的数学成绩,从中抽取500名考生的数学成绩进行统计分析,在这个问题中,下列说法:①这1万名考生的中考数学成绩的全体是总体;②每个考生是个体;③500名考生是总体的一个样本;④样本容量是500.其中说法正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.下列调查中,适合采用全面调查(普查)方式的是( )
| A. | 对长江水质量情况的调查 | |
| B. | 对端午节期间市场上粽子质量情况的调查 | |
| C. | 对某班45名学生身高情况的调查 | |
| D. | 对某批灯泡的使用寿命的调查 |
15.二次根式$\sqrt{x-3}$中字母x的取值范围是( )
| A. | x<3 | B. | x≤3 | C. | x>3 | D. | x≥3 |
16.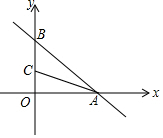 在平面直角坐标系中,已知一次函数y=-$\frac{3}{4}$x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
在平面直角坐标系中,已知一次函数y=-$\frac{3}{4}$x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
 在平面直角坐标系中,已知一次函数y=-$\frac{3}{4}$x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
在平面直角坐标系中,已知一次函数y=-$\frac{3}{4}$x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )| A. | (0,3) | B. | (0,$\frac{4}{3}$) | C. | (0,$\frac{8}{3}$) | D. | (0,$\frac{7}{3}$) |
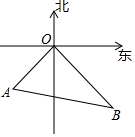 如图,甲轮船以24海里/小时的速度离开港口O向东南方向航行,乙轮船同时同地以18海里/小时的速度向西南方向航行,已知他们离开港口半小时后分别到达B,A两地,求A,B两地之间的距离.
如图,甲轮船以24海里/小时的速度离开港口O向东南方向航行,乙轮船同时同地以18海里/小时的速度向西南方向航行,已知他们离开港口半小时后分别到达B,A两地,求A,B两地之间的距离.