题目内容
6．下列命题中，为真命题的是（ ）| A． | 如果-2x＞-2，那么x＞1 | B． | 如果a2=b2，那么a3=b3 | ||
| C． | 面积相等的三角形全等 | D． | 如果a∥b，b∥c，那么a∥c |
分析 根据不等式的性质、全等三角形的判定、平行线的判定即可得出结论．
解答 解：A、如果-2x＞-2，那么x＞1；假命题；
B、如果a2=b2，那么a3=b3；假命题；
C、面积相等的三角形全等；假命题；
D、如果a∥b，b∥c，那么a∥c；真命题；
故选：D．
点评 本题考查了命题与定理；熟记不等式的性质、全等三角形的判定、平行线的判定是解决问题的关键．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
16．
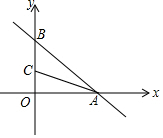在平面直角坐标系中，已知一次函数y=-$\frac{3}{4}$x+6与x，y轴分别交于A，B两点，点C（0，n）是y轴上一点，把坐标平面沿直线AC折叠，点B刚好落在x轴上，则点C的坐标是（ ）
在平面直角坐标系中，已知一次函数y=-$\frac{3}{4}$x+6与x，y轴分别交于A，B两点，点C（0，n）是y轴上一点，把坐标平面沿直线AC折叠，点B刚好落在x轴上，则点C的坐标是（ ）| A． | （0，3） | B． | （0，$\frac{4}{3}$） | C． | （0，$\frac{8}{3}$） | D． | （0，$\frac{7}{3}$） |
17．下列计算正确的是（ ）
| A． | x+x2=x3 | B． | x2•x3=x6 | C． | x9÷x3=x3 | D． | （x3）2=x6 |
14．
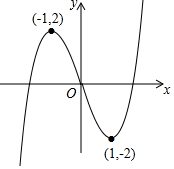函数y=x3-3x的图象如图所示，则以下关于该函数图象及其性质的描述正确的是（ ）
函数y=x3-3x的图象如图所示，则以下关于该函数图象及其性质的描述正确的是（ ）| A． | 函数最大值为2 | B． | 函数图象最低点为（1，-2） | ||
| C． | 函数图象关于原点对称 | D． | 函数图象关于y轴对称 |
11．已知P1（-3，y1），P2（2，y2）是一次函数y=-x-1的图象上的两个点，则y1，y2的大小关系是（ ）
| A． | y1=y2 | B． | y1＜y2 | C． | y1＞y2 | D． | 不能确定 |
18．下列轴对称图形中，对称轴条数最多的图形是（ ）
| A． | 等腰三角形 | B． | 正三角形 | C． | 菱形 | D． | 等腰梯形 |
10．
为了让更多的失学儿童重返校园，某社区组织“献爱心手拉手”捐款活动．对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）．已知A、B两组捐款户数的比为1：5．
捐款户数分组统计表
请结合以上信息解答下列问题．
（1）a=2，本次调查样本的容量是50；
（2）补全“捐款户数分组统计图1”，“捐款户数分组统计图2”中B组扇形圆心角度数为72°；
（3）若该社区有500户住户，请根据以上信息，估计全社区捐款不少于300元的户数180户．
为了让更多的失学儿童重返校园，某社区组织“献爱心手拉手”捐款活动．对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）．已知A、B两组捐款户数的比为1：5．捐款户数分组统计表
| 组别 | 捐款额（x）元 | 户数 |
| A | 1≤x＜100 | a |
| B | 100≤x＜200 | 10 |
| C | 200≤x＜300 | |
| D | 300≤x＜400 | |
| E | x≥400 |
（1）a=2，本次调查样本的容量是50；
（2）补全“捐款户数分组统计图1”，“捐款户数分组统计图2”中B组扇形圆心角度数为72°；
（3）若该社区有500户住户，请根据以上信息，估计全社区捐款不少于300元的户数180户．